Método de Reducción - Sistema de Ecuaciones Lineales 3x3 | Ejercicio 1
Summary
TLDREste video explica detalladamente el método de reducción o eliminación para resolver sistemas de ecuaciones lineales. A través de un proceso paso a paso, se enseña cómo eliminar variables, trabajar con multiplicaciones y sumas o restas de ecuaciones para simplificar el sistema. Finalmente, se encuentra la solución para las tres variables: x = 1, y = 2 y z = 3, y se verifica la exactitud de las soluciones sustituyéndolas en las ecuaciones originales. Este enfoque es útil para resolver ecuaciones con más de dos variables de forma ordenada y efectiva.
Takeaways
- 😀 La reducción es un método útil para resolver sistemas de ecuaciones, donde las ecuaciones deben estar ordenadas con las variables en el mismo orden.
- 😀 Es esencial numerar las ecuaciones para llevar un registro organizado y claro del proceso de resolución.
- 😀 El primer paso es trabajar con pares de ecuaciones, como la ecuación 1 con la ecuación 2, y la ecuación 1 con la ecuación 3.
- 😀 Se debe seleccionar una variable (en este caso, x) y utilizar operaciones de multiplicación o división para que los coeficientes de esa variable sean iguales pero de signo opuesto.
- 😀 La multiplicación de ecuaciones se hace tomando el coeficiente de una ecuación y multiplicando la otra por dicho número, asegurándose de cambiar el signo si es necesario.
- 😀 Tras la multiplicación, se suman o restan los términos semejantes, eliminando una de las variables (en este caso, x).
- 😀 Al eliminar la variable x, obtenemos una nueva ecuación que solo contiene las variables restantes (y, z).
- 😀 Luego, se repite el proceso de reducción con las variables restantes, en este caso, con la variable z, para obtener una nueva ecuación que solo tenga una variable.
- 😀 A través de la multiplicación por el coeficiente adecuado, se eliminan las variables restantes, obteniendo una ecuación con una sola variable que se puede resolver.
- 😀 Una vez resuelto el valor de una variable, se sustituyen los valores obtenidos en las ecuaciones originales para encontrar las otras variables.
- 😀 Finalmente, se comprueba la validez de las soluciones sustituyendo los valores encontrados en las ecuaciones originales para verificar que se cumplen todas las igualdades.
Q & A
¿Cuál es el primer paso al aplicar el método de reducción?
-El primer paso es ordenar las ecuaciones de manera que primero aparezca la variable x, luego la variable y, y finalmente la variable z. Después, se enumeran las ecuaciones para una resolución más ordenada.
¿Qué se debe hacer después de ordenar las ecuaciones?
-Una vez ordenadas, se copian las ecuaciones por separado en pares: la ecuación 1 con la ecuación 2, y la ecuación 1 con la ecuación 3. Esto facilita la aplicación de reducción.
¿Cómo se selecciona la variable a eliminar en el método de reducción?
-Se selecciona una variable, en este caso la variable x. Luego, se realizan multiplicaciones o divisiones para hacer que los coeficientes de esta variable sean iguales pero con signo opuesto.
¿Qué operación se realiza con las ecuaciones después de ajustar los coeficientes?
-Se multiplican las ecuaciones según los coeficientes elegidos para igualarlos con signo opuesto. Posteriormente, se suman o restan los términos semejantes, eliminando la variable seleccionada.
¿Por qué se llama al método de reducción como eliminación?
-Este método se llama 'eliminación' porque, mediante operaciones, se elimina una de las variables en cada paso, lo que facilita la resolución del sistema de ecuaciones.
¿Qué se hace después de eliminar una variable en el sistema de ecuaciones?
-Después de eliminar una variable, se obtiene una nueva ecuación con una o dos variables menos, lo que permite continuar resolviendo el sistema mediante los mismos principios de eliminación.
¿Cómo se resuelve el sistema después de obtener una ecuación con una sola variable?
-Una vez que se obtiene una ecuación con una sola variable, se despeja dicha variable. Luego, se reemplaza el valor encontrado en las ecuaciones anteriores para calcular las otras variables.
¿Qué ocurre cuando se obtiene un sistema de ecuaciones 2x2?
-Cuando se obtiene un sistema 2x2, se aplica nuevamente el método de reducción seleccionando una de las variables y realizando operaciones similares para eliminar una variable y resolver el sistema.
¿Qué se hace después de encontrar el valor de una variable?
-Una vez que se encuentra el valor de una variable, se reemplaza este valor en las ecuaciones originales para encontrar los valores de las otras variables. Este proceso se repite hasta resolver todo el sistema.
¿Cómo se verifica que las soluciones encontradas son correctas?
-Para verificar las soluciones, se sustituyen los valores obtenidos en las ecuaciones originales y se comprueba que ambas partes de cada ecuación sean iguales. Si se cumplen todas las igualdades, las soluciones son correctas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

01. Sistemas de ecuaciones lineales, 2 variables | Álgebra Lineal

Sistema de Ecuaciones 2x2 - Método de Eliminación o Reducción

Matemáticas Video 2 8
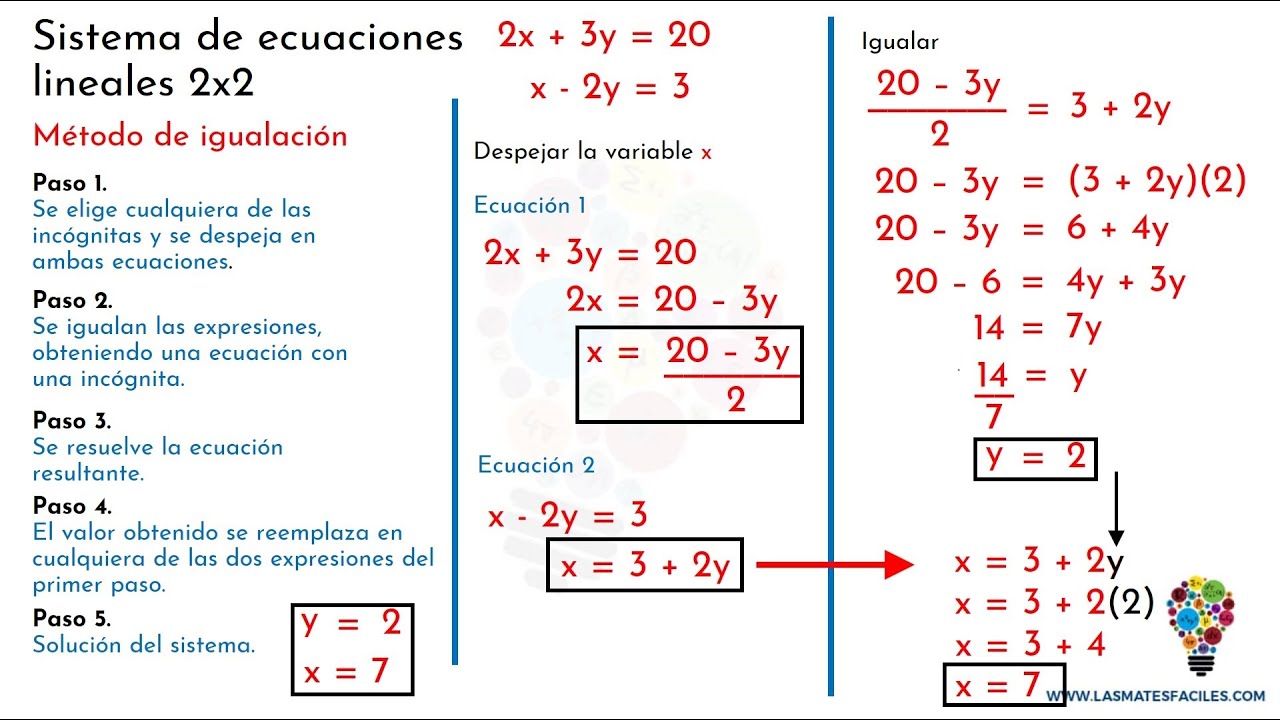
Sistemas de Ecuaciones 2x2 - Método de Igualación

09. ¿Qué es un sistema de ecuaciones lineales con dos incógnitas?

✅ Sistema de Ecuaciones Lineales [ Método de Eliminación ] - Ejemplos Resueltos #1
5.0 / 5 (0 votes)
