Why Single Layered Perceptron Cannot Realize XOR Gate
Summary
TLDRIn this video, the instructor explains why a single-layer perceptron (SLP) cannot solve the XOR problem. Using a graphical representation, the lecturer shows that the XOR function, which is not linearly separable, cannot be divided into two distinct categories (0 and 1) using a single line. Despite the perceptron’s structure of two inputs, weights, a bias, and an output, it can only classify linearly separable data. The video emphasizes the limitations of SLPs and highlights the need for more complex models, like multi-layer perceptrons, to handle non-linear problems like XOR.
Takeaways
- 😀 A single-layer perceptron (SLP) can only solve linearly separable problems.
- 😀 The XOR problem is a classic example of a non-linearly separable problem that cannot be solved by an SLP.
- 😀 The perceptron consists of an input layer with two inputs (X and Y), weights (W1, W2), and a bias term.
- 😀 The output of the perceptron is calculated using the weighted sum of the inputs and the bias: T = (X * W1) + (Y * W2) + B.
- 😀 A perceptron makes predictions by classifying data into two categories, such as a circle or a triangle.
- 😀 The XOR truth table involves four possible input combinations and produces binary outputs (0 or 1).
- 😀 When plotted, the XOR outputs cannot be separated by a single straight line on a graph, making it impossible for an SLP to classify them correctly.
- 😀 Even when attempting to draw a line to separate the XOR outputs, one of the points will always be misclassified.
- 😀 The inability to draw a single line to separate XOR’s outputs demonstrates why SLPs fail to solve non-linear problems.
- 😀 Multi-layer perceptrons (MLPs) are required to solve non-linearly separable problems like XOR, as they can create more complex decision boundaries.
Q & A
What is the main topic of the lecture in the provided transcript?
-The lecture explains why a single-layer perceptron cannot realize the XOR function, discussing the limitations of single-layer perceptrons in handling non-linearly separable data.
What is a single-layer perceptron (SLP)?
-A single-layer perceptron is a type of neural network consisting of an input layer, a set of weights, a bias, and an output layer. It is used to predict binary outcomes based on input features.
How does a single-layer perceptron compute its output?
-The perceptron computes the output as a weighted sum of the inputs, plus a bias term. The output is calculated as: T = (X * W1) + (Y * W2) + B, where X and Y are the inputs, W1 and W2 are weights, and B is the bias.
What does it mean for data to be 'linearly separable'?
-Data is considered linearly separable if it can be divided into distinct classes by a straight line (in 2D) or a hyperplane (in higher dimensions). This means that the data points of different classes do not overlap.
Why can’t a single-layer perceptron solve the XOR problem?
-The XOR problem cannot be solved by a single-layer perceptron because the XOR function is not linearly separable. No straight line can separate the output values of the XOR truth table correctly.
How is the XOR truth table represented in the context of the perceptron?
-In the context of the perceptron, the XOR truth table is plotted on a 2D graph where the horizontal axis represents X, the vertical axis represents Y, and the output (T) is shown as either 0 (red circle) or 1 (green circle).
What does the failure to separate XOR data with a straight line signify?
-The failure to separate XOR data with a straight line indicates that the data points are not linearly separable, meaning a simple perceptron cannot classify them correctly. This is a limitation of single-layer perceptrons.
Can you describe the visual representation of the XOR truth table on a 2D graph?
-On a 2D graph, the XOR truth table is represented as follows: (0, 0) → red circle (0), (0, 1) → green circle (1), (1, 0) → green circle (1), and (1, 1) → red circle (0). The goal is to separate the red and green circles with a line, which is impossible with a single-layer perceptron.
What is the significance of the perceptron failing to classify XOR correctly?
-The significance of the perceptron failing to classify XOR correctly highlights the limitations of single-layer perceptrons. It emphasizes the need for more complex models, like multi-layer perceptrons, to handle problems that require non-linear separability.
What can be used to solve the XOR problem, if not a single-layer perceptron?
-To solve the XOR problem, a multi-layer perceptron (MLP) or a neural network with hidden layers can be used. These models are capable of learning non-linear decision boundaries and can handle the XOR problem successfully.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Perceptron Rule to design XOR Logic Gate Solved Example ANN Machine Learning by Mahesh Huddar

Resolver ecuaciones exponenciales con logaritmos | Ejemplo 1
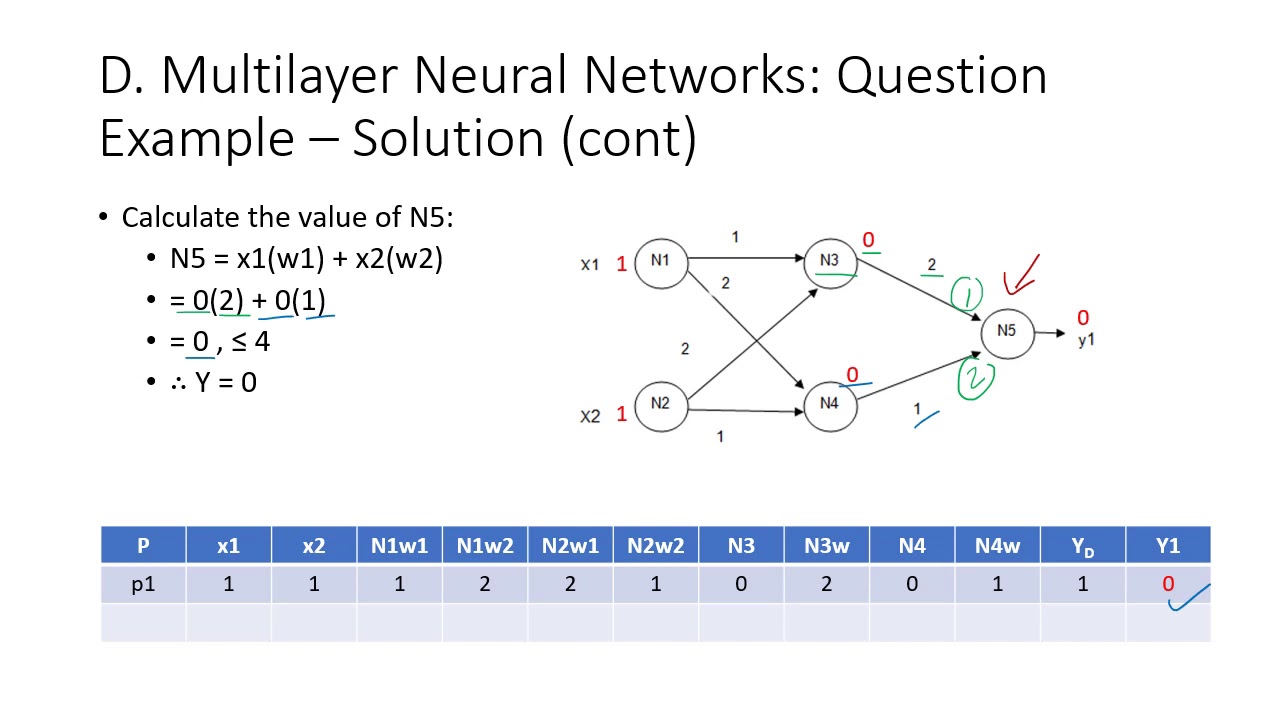
Topic 3D - Multilayer Neural Networks

Taxonomy of Neural Network

Manipulating the Trig Ratios in Geometry (example question)

Solución de problemas con Ecuaciones de Primer Grado | Ejemplo 5
5.0 / 5 (0 votes)