Sistema de Ecuaciones 2x2 - Método de Eliminación o Reducción
Summary
TLDREn este vídeo se enseña cómo resolver sistemas de ecuaciones lineales 2x2 utilizando el método de eliminación o reducción. Se recomienda la aplicación 'Sistema de ecuaciones 2x2' para dispositivos Android, que permite resolver ecuaciones por diferentes métodos. El ejemplo trabajado muestra cómo, al sumar ambas ecuaciones, se elimina una variable, facilitando la obtención de la solución. Posteriormente, se reemplaza el valor encontrado en una de las ecuaciones iniciales para resolver la otra variable, verificando la solución en ambas ecuaciones.
Takeaways
- 📚 Aprenderemos a resolver sistemas de ecuaciones lineales 2x2 usando el método de eliminación o reducción.
- 🔢 Un sistema 2x2 consiste de dos ecuaciones con dos incógnitas.
- 📱 Hay una aplicación para dispositivos Android que ayuda a resolver sistemas de ecuaciones 2x2.
- 🔗 Se recomienda suscribirse al canal de YouTube para seguir aprendiendo.
- 🧮 El método de eliminación busca combinar ecuaciones para eliminar una de las variables.
- 📝 Se muestra un ejemplo específico para resolver usando el método de eliminación.
- ➖ Para eliminar una variable, se suman o restan ecuaciones multiplicadas por coeficientes adecuados.
- ✅ Se explica que si la combinación no funciona al primer intento, se deben realizar ajustes para lograr la eliminación.
- 🔄 Se describe el proceso paso a paso, desde preparar las ecuaciones hasta resolver la incógnita resultante.
- 🔄 Una vez resuelta una incógnita, su valor se reemplaza en una de las ecuaciones originales para encontrar la otra.
- 🔍 Se enfatiza la importancia de verificar la solución obtenida reemplazando los valores en las ecuaciones originales.
Q & A
¿Qué método se enseña en el guion para resolver sistemas de ecuaciones lineales 2x2?
-Se enseña el método de eliminación o reducción para resolver sistemas de ecuaciones lineales 2x2.
¿Cuál es el objetivo principal del método de eliminación en un sistema de ecuaciones 2x2?
-El objetivo principal es eliminar una de las incógnitas para poder resolver la ecuación en una sola variable.
¿Qué aplicación se menciona en el guion para resolver sistemas de ecuaciones 2x2?
-Se menciona una aplicación llamada 'sistema de ecuaciones 2x2' disponible para dispositivos Android.
¿Cómo se puede acceder a la aplicación para resolver sistemas de ecuaciones 2x2 mencionada en el guion?
-El enlace de descarga de la aplicación se encuentra en la descripción del vídeo.
¿Qué métodos de resolución son compatibles con la aplicación para sistemas de ecuaciones 2x2?
-La aplicación permite resolver sistemas de ecuaciones 2x2 mediante el método de eliminación, el método de igualación, sustitución y la regla de Cramer.
¿Cuál es el primer paso para preparar las ecuaciones antes de aplicar el método de eliminación?
-El primer paso es multiplicar las ecuaciones por números adecuados para que se puedan sumar o restar de forma que se elimine una de las incógnitas.
¿Cómo se realiza la preparación de las ecuaciones para eliminar el término 2x en el ejemplo del guion?
-Se multiplica la segunda ecuación por -2 para que los términos 2x se anulen al sumar ambas ecuaciones.
¿Cuál es la ecuación resultante después de sumar las ecuaciones preparadas en el método de eliminación?
-La ecuación resultante es 7y = 14 después de sumar las ecuaciones preparadas.
¿Cómo se resuelve la ecuación resultante una vez que se ha eliminado una de las incógnitas?
-Se resuelve la ecuación resultante dividiendo ambos lados de la ecuación por el coeficiente de la incógnita que quedó, en este caso, dividiendo 14 entre 7 para encontrar el valor de y.
¿Cómo se verifica la solución del sistema de ecuaciones una vez que se han encontrado los valores de las incógnitas?
-Se reemplaza el valor de la incógnita resuelta en cualquiera de las ecuaciones iniciales y se verifica que se cumpla la igualdad en ambos lados de la ecuación.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
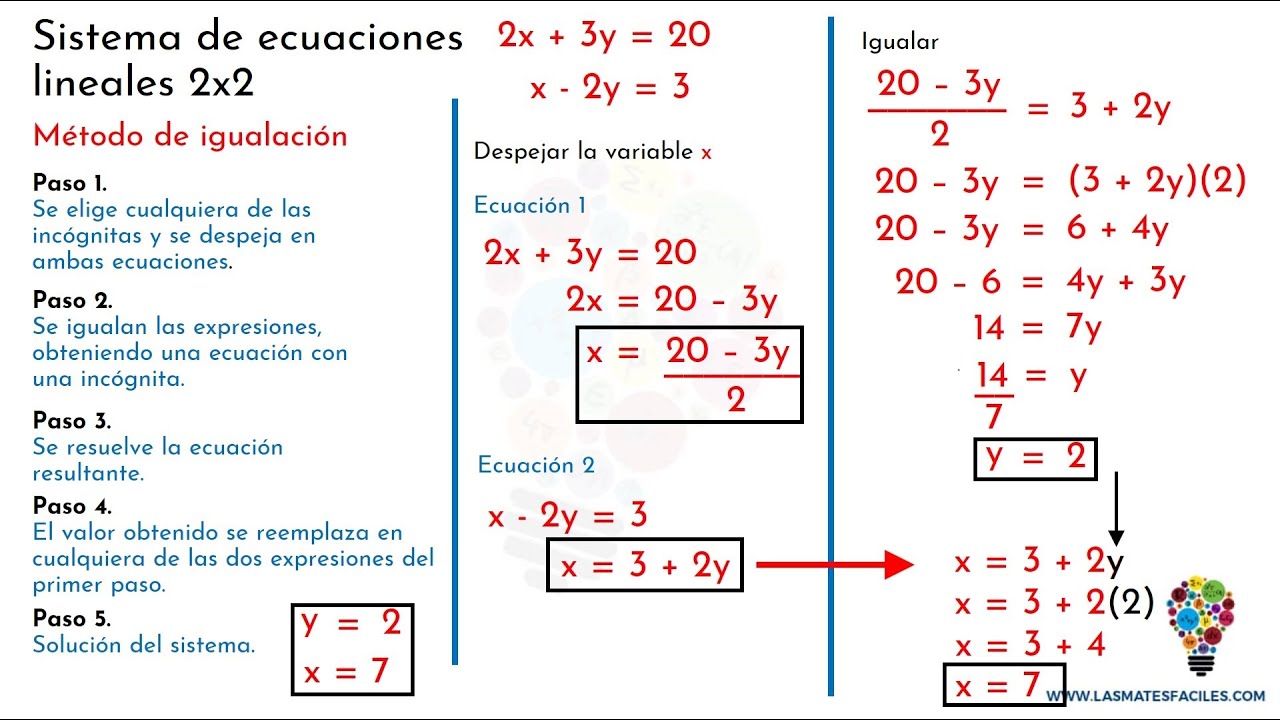
Sistemas de Ecuaciones 2x2 - Método de Igualación

Método de Reducción - Sistema de Ecuaciones Lineales 3x3 | Ejercicio 1

Solución de problemas con Sistemas de Ecuaciones Lineales 2x2 | Ejemplo 3

✅ Sistema de Ecuaciones Lineales [ Método de Eliminación ] - Ejemplos Resueltos #1

01. Sistemas de ecuaciones lineales, 2 variables | Álgebra Lineal

Sistema de ecuaciones 2x2. Método de suma y resta.Álgebra
5.0 / 5 (0 votes)
