Las distribuciones Bernoulli, binomial y normal
Summary
TLDREn este video, el presentador explica tres distribuciones importantes: la distribución Bernoulli, la binomial y la normal. Comienza describiendo la distribución Bernoulli como una variable binaria con valores de 0 o 1, ejemplificando con el lanzamiento de una moneda. Luego, introduce la distribución binomial, que surge de realizar varios lanzamientos de la moneda, mostrando cómo las probabilidades cambian con el número de intentos. Utilizando el triángulo de Pascal en Excel, muestra cómo la distribución binomial se aproxima a la distribución normal a medida que aumentan los intentos, dando forma a la clásica campana de Gauss.
Takeaways
- 😀 La distribución Bernoulli es una variable binaria que toma valores de 0 o 1, con una probabilidad de éxito que se define como 'p'.
- 😀 Un ejemplo común de la distribución Bernoulli es el lanzamiento de una moneda, donde la probabilidad de cara o cruz es 50% cada una.
- 😀 La distribución binomial es una colección de variables Bernoulli y se utiliza para modelar el número de éxitos en una secuencia de ensayos independientes.
- 😀 En la distribución binomial, el número de ensayos (por ejemplo, 10 lanzamientos) influye en la forma de la distribución.
- 😀 El triángulo de Pascal es una herramienta matemática que puede ayudar a entender la distribución binomial y su relación con los coeficientes binomiales.
- 😀 En el triángulo de Pascal, cada número es la suma de los dos números directamente por encima de él, lo cual es útil para calcular probabilidades en la distribución binomial.
- 😀 A medida que aumentan los ensayos (lanzamientos de monedas), la distribución binomial empieza a formar una forma de campana, que se asemeja a la distribución normal.
- 😀 La distribución normal se obtiene a medida que el número de ensayos en una distribución binomial tiende al infinito, formando una curva simétrica.
- 😀 La distribución normal tiene una caída constante en las colas, lo que significa que las probabilidades de valores extremos se reducen de manera predecible.
- 😀 Es importante entender que una distribución binomial es una colección de variables Bernoulli, pero cuando el número de ensayos crece lo suficiente, la distribución binomial se aproxima a la normal.
Q & A
¿Qué es una variable de Bernoulli y cómo se utiliza?
-Una variable de Bernoulli es una variable binaria que puede tomar dos valores: 0 o 1. La probabilidad de que la variable tome el valor 1 se define por un parámetro, como en el caso del lanzamiento de una moneda, donde la probabilidad de obtener cara (1) es del 50% y de obtener cruz (0) también es del 50%.
¿Qué es una distribución binomial?
-Una distribución binomial es el resultado de realizar múltiples experimentos de Bernoulli. Por ejemplo, al lanzar una moneda 10 veces, la distribución binomial nos ayuda a calcular las probabilidades de obtener diferentes cantidades de caras o cruces en esos 10 lanzamientos.
¿Cómo se interpreta la distribución binomial en el caso del lanzamiento de una moneda 10 veces?
-En una distribución binomial con 10 lanzamientos de una moneda, se calcula la probabilidad de obtener 0, 1, 2... hasta 10 caras. Por ejemplo, la probabilidad de obtener 5 caras y 5 cruces podría ser del 25%, siendo este el evento más probable en este caso.
¿Qué es el triángulo de Pascal y cómo se relaciona con la distribución binomial?
-El triángulo de Pascal es una estructura matemática en la que cada número es la suma de los dos números directamente encima de él. Este triángulo está directamente relacionado con la distribución binomial, ya que los coeficientes binomiales, que se utilizan para calcular las probabilidades en la distribución binomial, están contenidos en las filas del triángulo de Pascal.
¿Cómo se visualiza la transición de la distribución binomial a la distribución normal?
-Al aumentar el número de lanzamientos (o experimentos) en una distribución binomial, la forma de la distribución se aproxima a una campana, lo que es característico de la distribución normal. Este fenómeno se observa al construir el triángulo de Pascal y graficar los resultados con un número elevado de experimentos.
¿Qué sucede cuando el número de lanzamientos en la distribución binomial tiende al infinito?
-Cuando el número de lanzamientos en una distribución binomial aumenta considerablemente, la forma de la distribución se aproxima a una distribución normal. Esta distribución normal es simétrica y tiene colas que caen de manera constante, lo que la hace muy representativa de fenómenos naturales.
¿Qué nos enseña el gráfico final del triángulo de Pascal con 47 lanzamientos?
-El gráfico final muestra cómo, con un número elevado de lanzamientos (como 47), la distribución binomial tiende a adoptar una forma de campana, lo que es característico de la distribución normal. Esto ilustra cómo las distribuciones binomiales se transforman en normales a medida que el número de intentos aumenta.
¿Por qué es importante entender la relación entre la distribución binomial y la normal?
-Es crucial entender esta relación porque la distribución binomial describe situaciones con resultados discretos y la distribución normal describe situaciones con resultados continuos. Al conocer cómo se transforma una en la otra, se pueden aplicar modelos más simples y continuos para describir fenómenos que originalmente se modelan con variables discretas.
¿Qué caracteriza a la distribución normal en términos de su forma?
-La distribución normal tiene una forma simétrica y de campana. Además, presenta colas que caen de manera constante a medida que nos alejamos de la media. Esta característica hace que sea una de las distribuciones más importantes y utilizadas en estadística y probabilidad.
¿Cuál es la importancia de los coeficientes binomiales en la distribución binomial?
-Los coeficientes binomiales, que se derivan del triángulo de Pascal, son fundamentales para calcular las probabilidades en la distribución binomial. Estos coeficientes indican cuántas maneras diferentes se pueden organizar los éxitos (por ejemplo, las caras) en un número dado de intentos, lo que permite calcular la probabilidad de obtener un número específico de éxitos.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
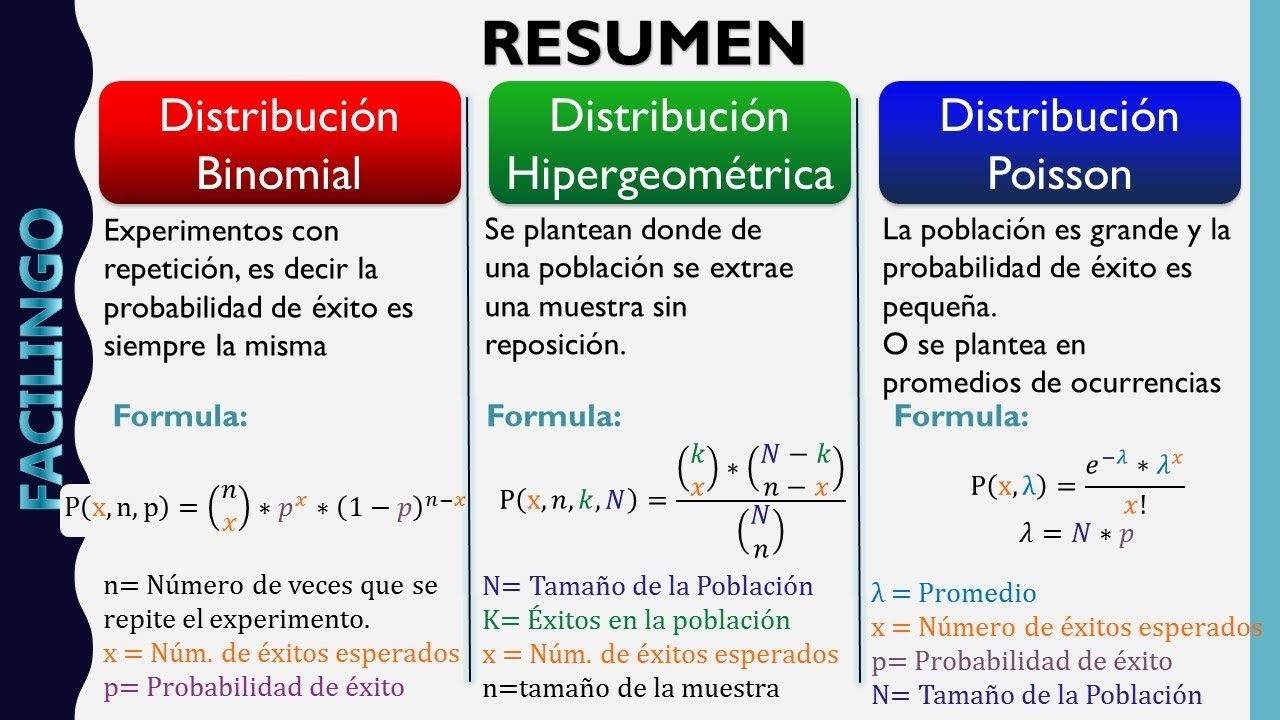
Distribuciones Discretas (Binomial, Hipergeometrica, Poisson)

Estandarización de una variable con distribución normal

Distribución de Bernoulli y Distribución Binomial

Distribución binomial | Ejercicio resuelto 2: representación mediante tabla y gráfica

Distribuciones marginales y condicionales a partir de una distribución conjunta

Asimetría y Curtosis
5.0 / 5 (0 votes)
