Problema 2 de MEZCLA
Summary
TLDREn este video, se resuelve un problema de mezclas donde se deben combinar dos soluciones de alcohol con concentraciones del 30% y 70% para obtener una mezcla con una concentración del 60%. Se utiliza una ecuación de balance de masas, donde se plantean las cantidades y concentraciones de cada solución. A través de los pasos de simplificación y resolución de la ecuación, se determina que se deben usar 30 litros de la solución al 30%. El video proporciona una explicación detallada de cómo resolver este tipo de problemas de mezclas de manera clara y comprensible.
Takeaways
- 😀 Se trata de un problema de mezcla de soluciones con diferentes concentraciones de alcohol.
- 😀 El objetivo es encontrar cuántos litros de una solución al 30% deben mezclarse con 90 litros de una solución al 70% para obtener una mezcla al 60%.
- 😀 La fórmula utilizada para resolver el problema es: cantidad1 * concentración1 + cantidad2 * concentración2 = cantidad mezcla * concentración mezcla.
- 😀 La incógnita en este problema es la cantidad de la solución al 30%, representada por 'x' litros.
- 😀 La ecuación planteada para resolver el problema es: x * 0.30 + 90 * 0.70 = (x + 90) * 0.60.
- 😀 El valor de 'x' representa la cantidad de la solución al 30% que debe mezclarse con la solución al 70%.
- 😀 Al resolver la ecuación, se obtiene x = 30, lo que significa que deben usarse 30 litros de la solución al 30%.
- 😀 El proceso de resolución implica despejar términos y aplicar la propiedad distributiva para simplificar la ecuación.
- 😀 La transposición de términos y la reducción de términos semejantes son pasos clave en la resolución de la ecuación.
- 😀 Finalmente, la respuesta a la pregunta es que se deben utilizar 30 litros de la solución de alcohol al 30% para obtener la mezcla deseada al 60%.
Q & A
¿Qué tipo de problema se está resolviendo en el video?
-Se está resolviendo un problema de mezclas de soluciones con diferentes concentraciones de alcohol.
¿Cuál es la fórmula que se utiliza para resolver el problema?
-La fórmula utilizada es: cantidad1 * concentración1 + cantidad2 * concentración2 = cantidad mezcla * concentración mezcla.
¿Qué representan los valores 'x' y '90' en la ecuación planteada?
-'x' representa la cantidad de litros de la solución al 30% que se deben mezclar, y '90' representa la cantidad de litros de la solución al 70%.
¿Cómo se determina la cantidad total de la mezcla?
-La cantidad total de la mezcla es la suma de las cantidades de ambas soluciones: 'x' litros de alcohol al 30% y 90 litros de alcohol al 70%.
¿Qué significa el 60% en la ecuación?
-El 60% es la concentración deseada de la mezcla final de alcohol después de mezclar las dos soluciones.
¿Qué se hace después de escribir la ecuación con todos los valores?
-Después de escribir la ecuación, se aplican las operaciones aritméticas, como la propiedad distributiva y la transposición de términos para despejar la incógnita 'x'.
¿Qué operación se realiza para simplificar la ecuación?
-Se realizan operaciones de multiplicación y luego transposición de términos para dejar todos los términos con 'x' en un lado y los números en el otro lado de la ecuación.
¿Qué sucede al resolver la ecuación?
-Al resolver la ecuación, se encuentra que el valor de 'x' es 30, lo que significa que se deben utilizar 30 litros de la solución de alcohol al 30%.
¿Cuál es el valor final de 'x' y qué implica?
-El valor final de 'x' es 30, lo que implica que se deben mezclar 30 litros de la solución al 30% con 90 litros de la solución al 70% para obtener una mezcla al 60%.
¿Cómo se verifica el resultado de la ecuación?
-El resultado se verifica sustituyendo el valor de 'x' en la ecuación original y comprobando que ambas partes de la igualdad sean iguales.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Concentración de las soluciones - %mm - Lección

Función Racional - Ejercicios Nivel 3 - Aplicaciones

[ QUIMICA FREE ] - SOLUCIONES II - Molaridad - Normalidad - Mezcla de soluciones

diluciones
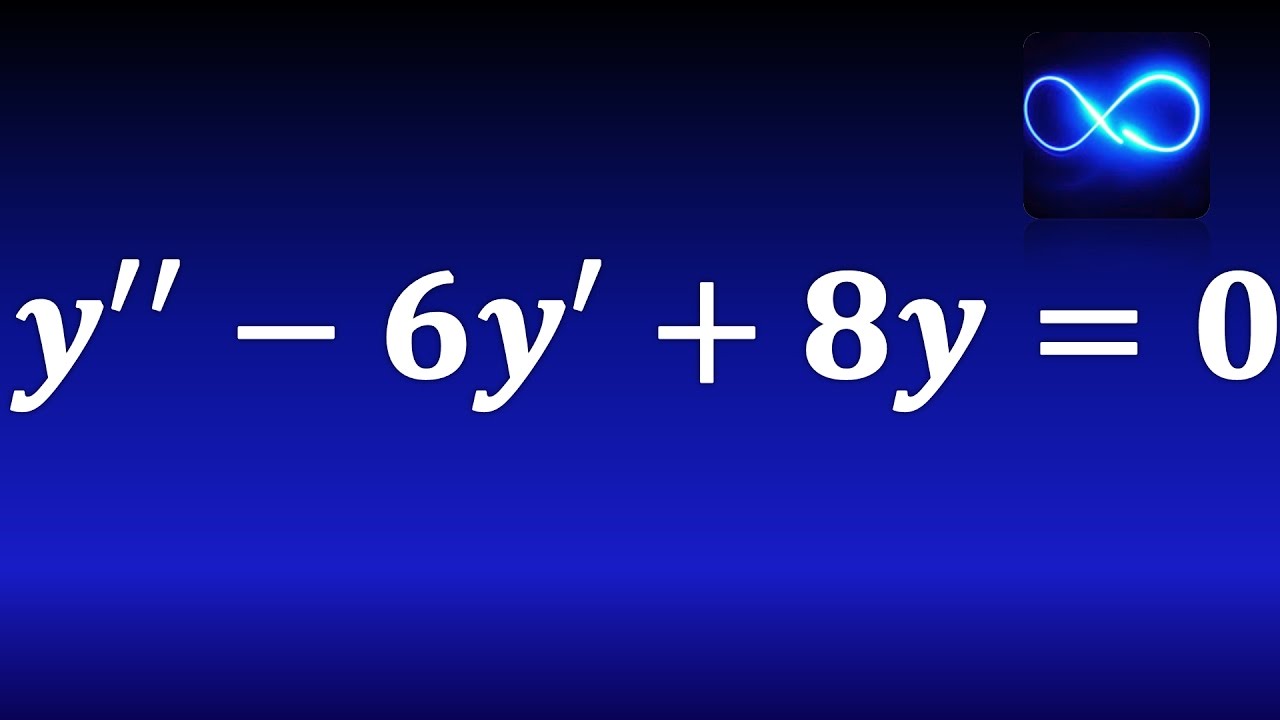
86. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO

COMO CALCULAR LA CONCENTRACIÓN DE UNA SOLUCIÓN. %m/m, %v/v, %m/v. SOLUCIONES 3. QUÍMICA CON IRWIN
5.0 / 5 (0 votes)
