Derivando funciones compuestas 1 | Cálculo | Khan Academy en Español
Summary
TLDRThis video explains how to find the derivative of the function f(x) = (cos(x))^3 using the chain rule. It walks through the process step by step, starting with the composition of two functions and how to apply the chain rule to differentiate them. The explanation is broken down into simpler concepts, such as deriving the function exterior and interior, using color-coded terms for clarity. The final result shows the derivative as -3cos(x)^2sin(x), with a focus on understanding the relationship between the functions and their derivatives. The tutorial is designed to help students grasp the concept of the chain rule more intuitively.
Please replace the link and try again.
Please replace the link and try again.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
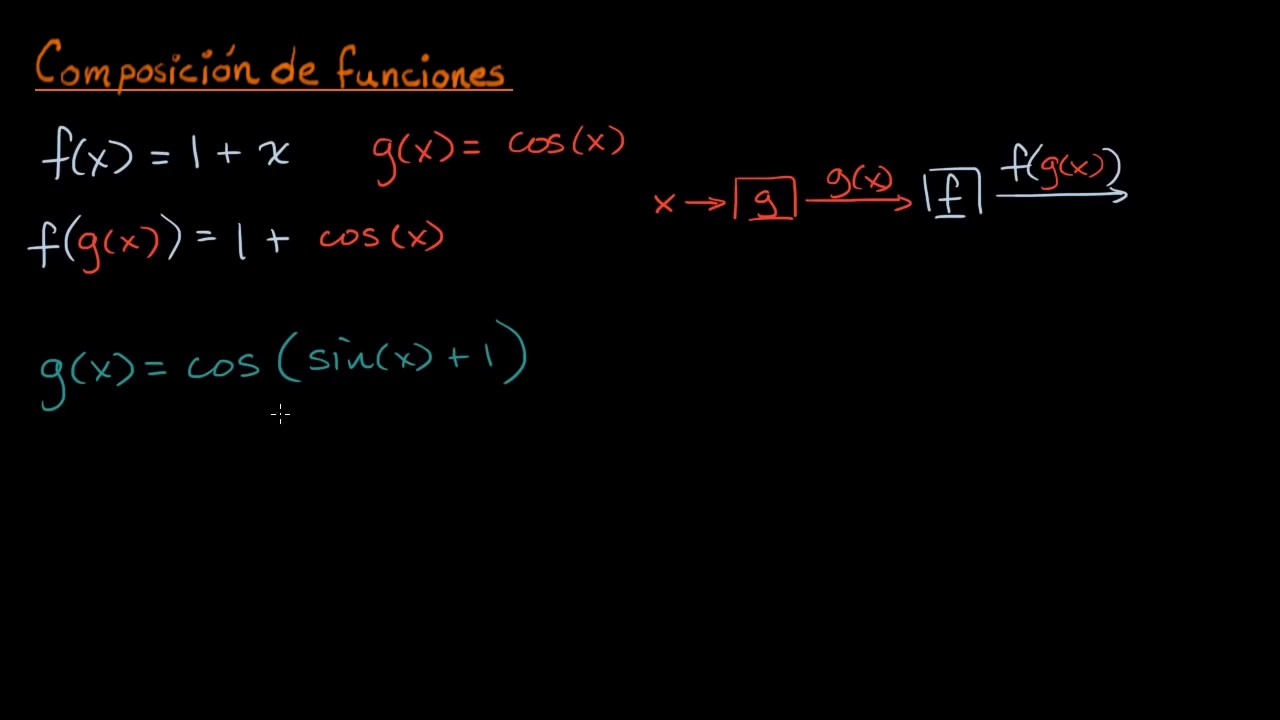
Reconocer una composición de funciones | Khan Academy en Español

Definition of the Derivative
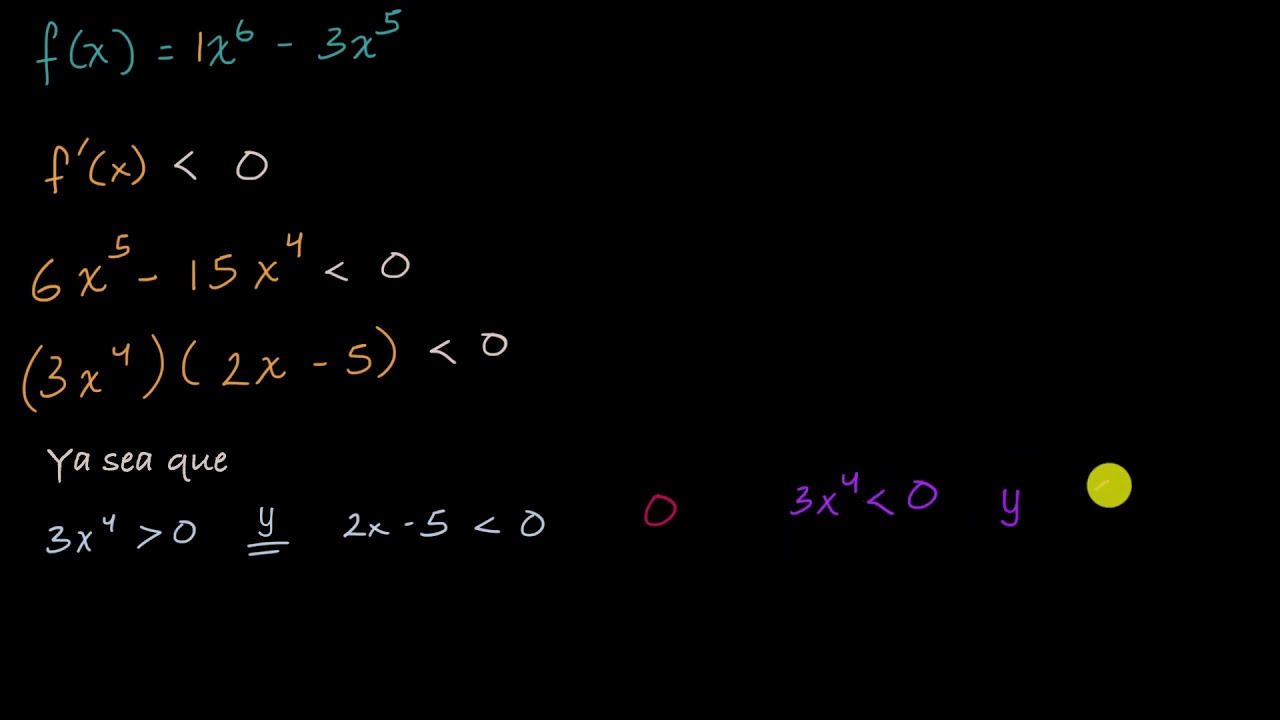
Encontrar el intervalo donde la función es decreciente | Cálculo

Composite Functions

Calculating slope of tangent line using derivative definition | Differential Calculus | Khan Academy
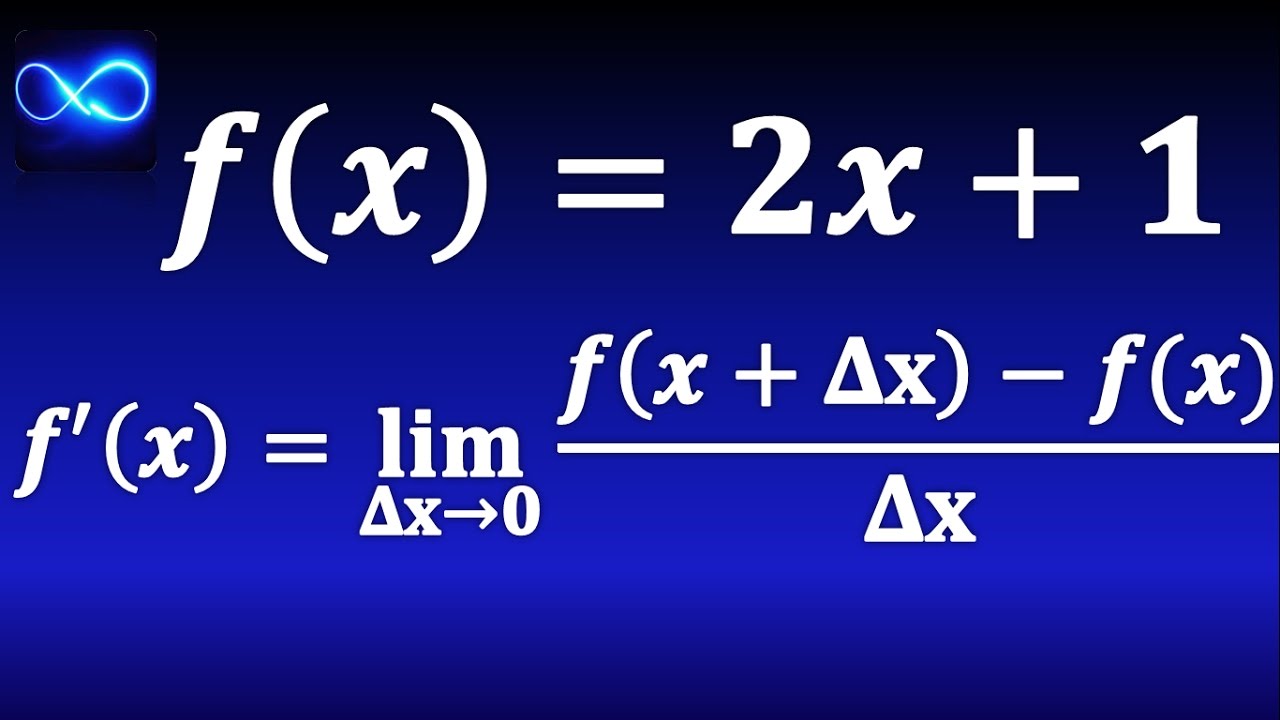
Derivative by increment method (By definition with limit)
5.0 / 5 (0 votes)