01. Derivative using definition as limit
Summary
TLDRIn this video, the presenter introduces the concept of calculating derivatives using the definition as a limit. The process is explained through a simple constant function, f(x) = 2, where the derivative is shown to be zero. The presenter walks viewers through the steps of applying the definition of a derivative, simplifying the expression, and concluding that the derivative of a constant function is always zero. The video encourages viewers to try the same process for other constant functions and offers further guidance in future videos.
Q & A
What is the main goal of the video?
-The main goal of the video is to explain how to calculate derivatives using the limit definition, specifically starting with a simple constant function.
What is a constant function?
-A constant function is a function where the output value remains the same, regardless of the input value for x. In the video, the example given is f(x) = 2.
How is the derivative of a function calculated using the limit definition?
-The derivative is calculated using the formula: limit as h approaches 0 of [f(x + h) - f(x)] / h. This is derived from the definition of the slope of a tangent line to a curve at a point.
Why is the derivative of a constant function zero?
-The derivative of a constant function is zero because, when applying the limit definition, the difference between f(x + h) and f(x) is always zero (since both are constant), and dividing zero by any value of h still results in zero.
What does f(x + h) represent in the limit definition of the derivative?
-In the limit definition, f(x + h) represents the value of the function at a point that is h units away from x.
How do you compute the derivative of a constant function step by step?
-To compute the derivative of a constant function, you substitute x + h into the function (which will still result in the same constant), subtract the original function value, and divide by h. The result simplifies to zero, and thus the derivative is zero.
What happens when you take the limit of a constant function’s derivative?
-When you take the limit of a constant function's derivative, the result is simply the constant value itself because there are no variables that change in the function. In this case, the derivative is zero.
Can you calculate the derivative of other constant functions using the same method?
-Yes, any constant function will have a derivative of zero, as the process described in the video applies to all constant functions. The difference between f(x + h) and f(x) will always be zero, leading to a derivative of zero.
What did the presenter suggest viewers do after watching this video?
-The presenter encouraged viewers to try calculating the derivative of the function f(x) = 5 using the same method and to check their result in the next video, where the full procedure will be demonstrated.
What additional resources did the presenter provide for further learning?
-The presenter mentioned providing a link to a course on limits in the video description for viewers who need to review the concept of limits, which is essential for understanding derivatives.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Episode 3: Bahas Turunan Lengkap dengan Visualisasi

KALKULUS | TURUNAN | APA ITU TURUNAN?
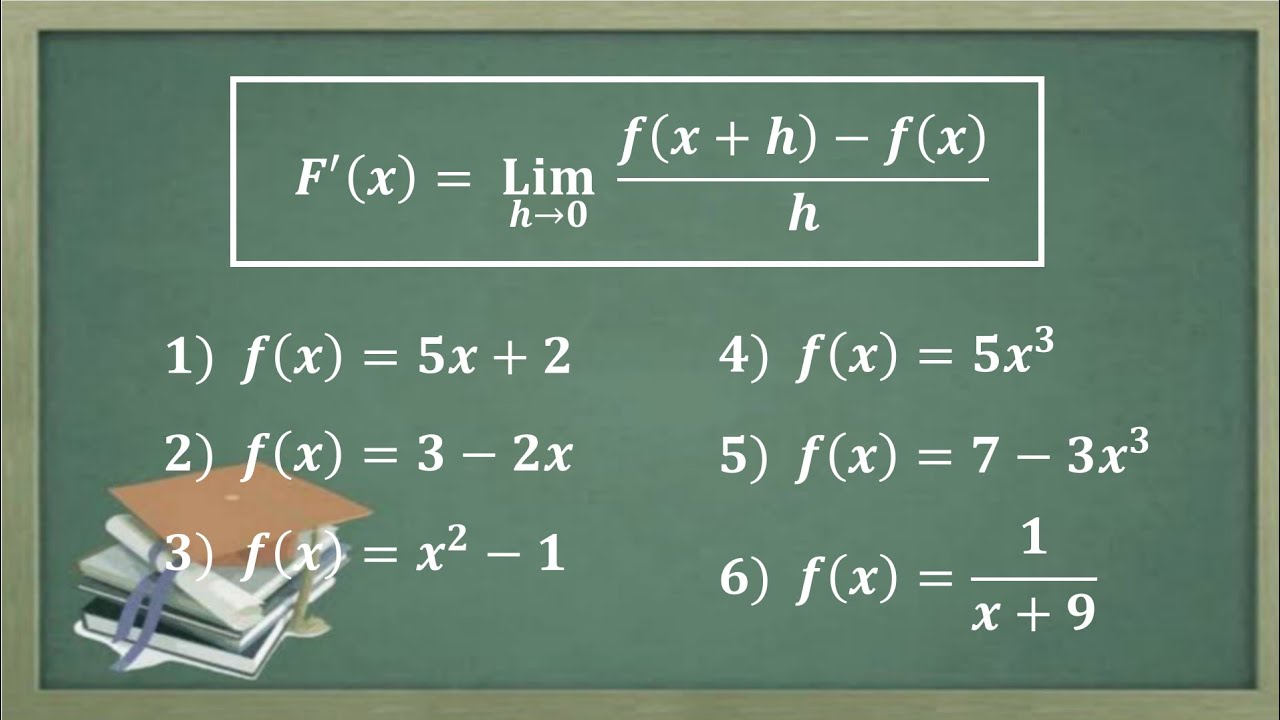
Turunan dengan menggunakan defnisi turunan Turunan menggunakan limit
Turunanfungsi Trigonometri Bag 1

Penerapan Turunan dalam kehidupan sehari-hari

Konsep Dasar Turunan Fungsi Aljabar Matematika Wajib Kelas 11 m4thlab
5.0 / 5 (0 votes)