101. OCR A Level (H046-H446) SLR15 - 1.4 Karnaugh maps part 4
Summary
TLDRThis video explains how to simplify Boolean expressions using four-input Karnaugh maps (K-maps). It covers the process of setting up a K-map, filling it with values based on the given Boolean expression, and then simplifying the expression by grouping terms into boxes. The video emphasizes using Gray codes for the correct sequence of variables and illustrates the step-by-step process of drawing optimal boxes. Two examples are worked through in detail, showing how to derive the simplified expressions. The video concludes with a reminder of a free Boolean algebra cheat sheet available for download, providing additional resources for revision.
Takeaways
- 😀 Karnaugh maps are a tool for simplifying Boolean expressions, and this video focuses on simplifying four-input Karnaugh maps.
- 😀 To understand four-input Karnaugh maps, it is assumed that the viewer has already watched previous videos in the series covering basic Karnaugh map concepts.
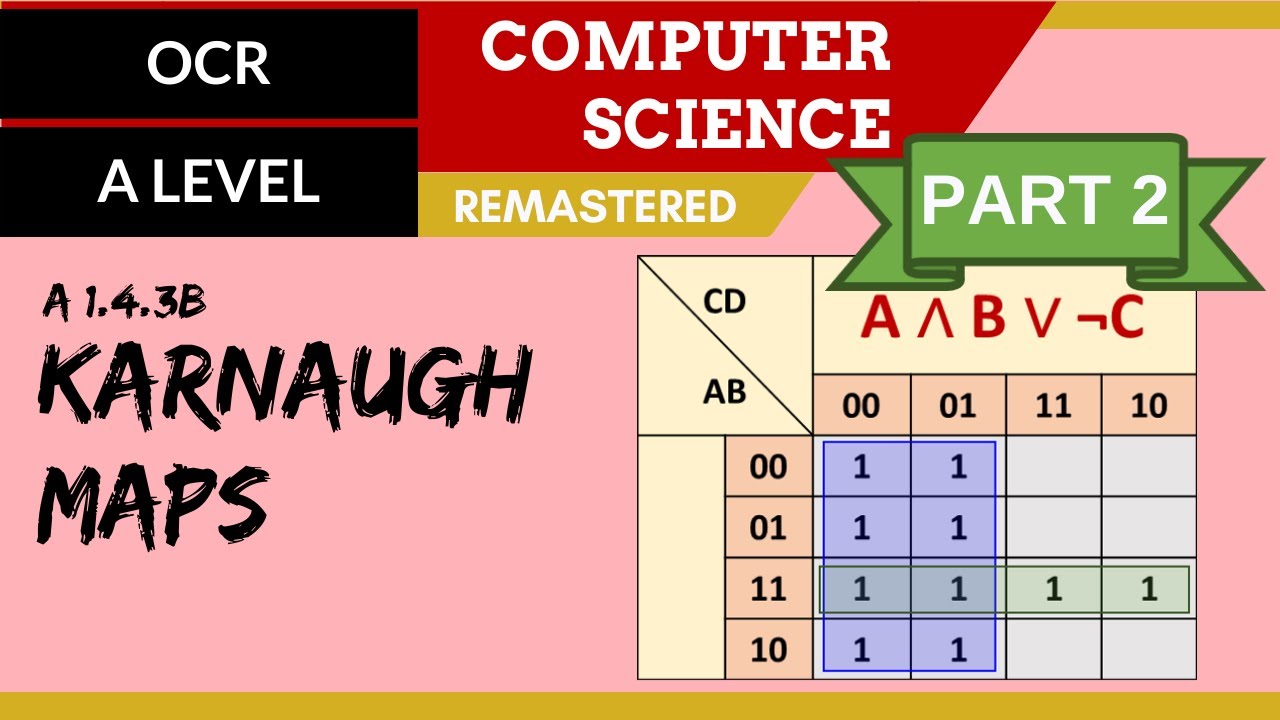
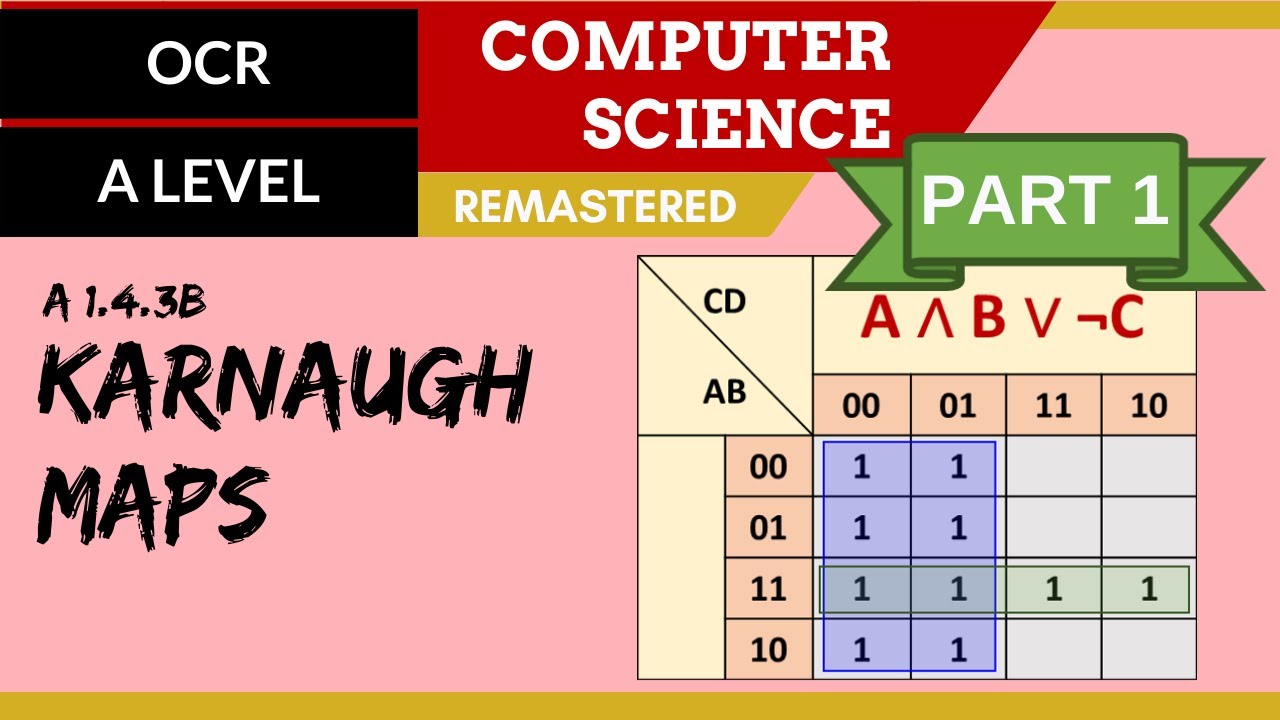
- 😀 A four-input Karnaugh map uses two variables along the top (A and B) and two along the side (C and D). The binary headings represent all possible states for the variables.
- 😀 The binary numbers in the headings of a Karnaugh map follow Gray codes, where only one digit changes between adjacent cells. This sequence is essential for map accuracy.
- 😀 When simplifying expressions, the different parts are placed into the Karnaugh map, with each part represented by ones in relevant cells.
- 😀 The simplification process involves grouping adjacent ones in boxes of sizes that maximize the number of simplified variables.
- 😀 In a simplification, we keep the variables that stay the same within each box, discarding those that change.
- 😀 The first example showed the expression 'not C and D or A and B,' where a simple grouping allowed for the expression to be kept as is, with no further simplification.
- 😀 A more complex example demonstrated how to simplify an expression like 'not A and B and C and D or not A and B and C or not D' by drawing boxes around ones and using Gray code rules.
- 😀 The simplified result from the second example was expressed as 'not D or (not A and B and C),' which is equivalent to 'not A and B and C or not D' in commutative form.
- 😀 The video concludes by introducing a free Boolean algebra cheat sheet, which includes logic gates, truth tables, and other essential material for further learning.
Q & A
What is the purpose of this video series on Karnaugh maps?
-The purpose of this video series is to teach viewers how to simplify Boolean expressions using Karnaugh maps, with a specific focus on simplifying four-input K-maps in the final video.
What assumption does the video make about the viewers' knowledge?
-The video assumes that viewers are already familiar with the content covered in the previous videos in the series. If not, the viewers are encouraged to watch those first.
What are Karnaugh maps used for?
-Karnaugh maps are used to simplify Boolean expressions by visually grouping cells of 1s, which helps in reducing the complexity of logical expressions.
How is the four-input Karnaugh map set up?
-A four-input Karnaugh map is set up by placing two variables across the top and two variables down the side. In the video, A and B are placed across the top, and C and D down the side.
What is the significance of Gray codes in Karnaugh maps?
-Gray codes are used for labeling the rows and columns of the Karnaugh map. They ensure that only one variable changes at a time between adjacent cells, which is important for grouping 1s in the map.
What is the process of placing parts of the Boolean expression into the Karnaugh map?
-The parts of the Boolean expression are placed into the Karnaugh map by identifying cells where the expression is true. Each part of the expression corresponds to a certain set of cells, and ones are placed in these cells.
What rule is followed to simplify the Karnaugh map?
-The simplification rule involves drawing boxes around groups of ones in the map. The boxes should be as large as possible and should contain a number of ones that is a power of 2.
How do you determine the simplified Boolean expression from the Karnaugh map?
-To determine the simplified Boolean expression, you examine the variables in each box and identify which variables remain constant within the group. The variables that do not change are kept in the simplified expression.
In the second example, what simplification is made from the large box of 8 ones?
-In the second example, the large box of 8 ones simplifies to 'NOT D' because only the variable D remains constant within the box, and the value is zero.
How is the second box in the second example simplified?
-The second box, which contains two ones, is simplified to 'NOT A AND B AND C' because A, B, and C remain constant in this box, while the variable D changes.
What is the final simplified expression in the second example?
-The final simplified expression in the second example is 'NOT D OR (NOT A AND B AND C)', which can also be written as '(NOT A AND B AND C) OR NOT D'.
What additional resource is provided at the end of the video?
-At the end of the video, viewers are directed to a website where they can download a free Boolean Algebra cheat sheet, which covers various topics such as Boolean algebra, logic gates, truth tables, and more.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

13 Karnaugh Map Menyederhanakan Fungsi Boolean - K-Map - Peta Karnaugh
99. OCR A Level (H046-H446) SLR15 - 1.4 Karnaugh maps part 2
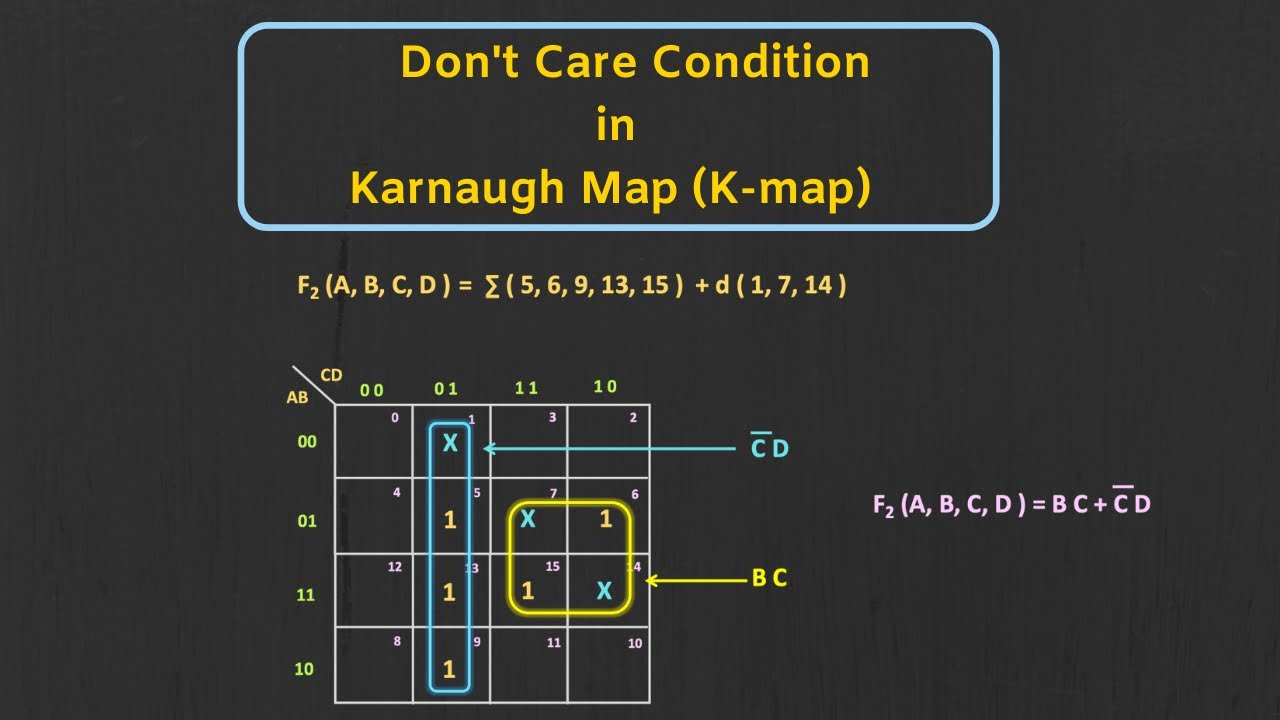
Don't Care Conditions in Karnaugh Map (with Solved Examples)

4 Variable K Map | Minimisation of given Function using K Map | By Mathur Sir
98. OCR A Level (H046-H446) SLR15 - 1.4 Karnaugh maps part 1

Quine-McCluskey Minimization Technique (Tabular Method)
5.0 / 5 (0 votes)