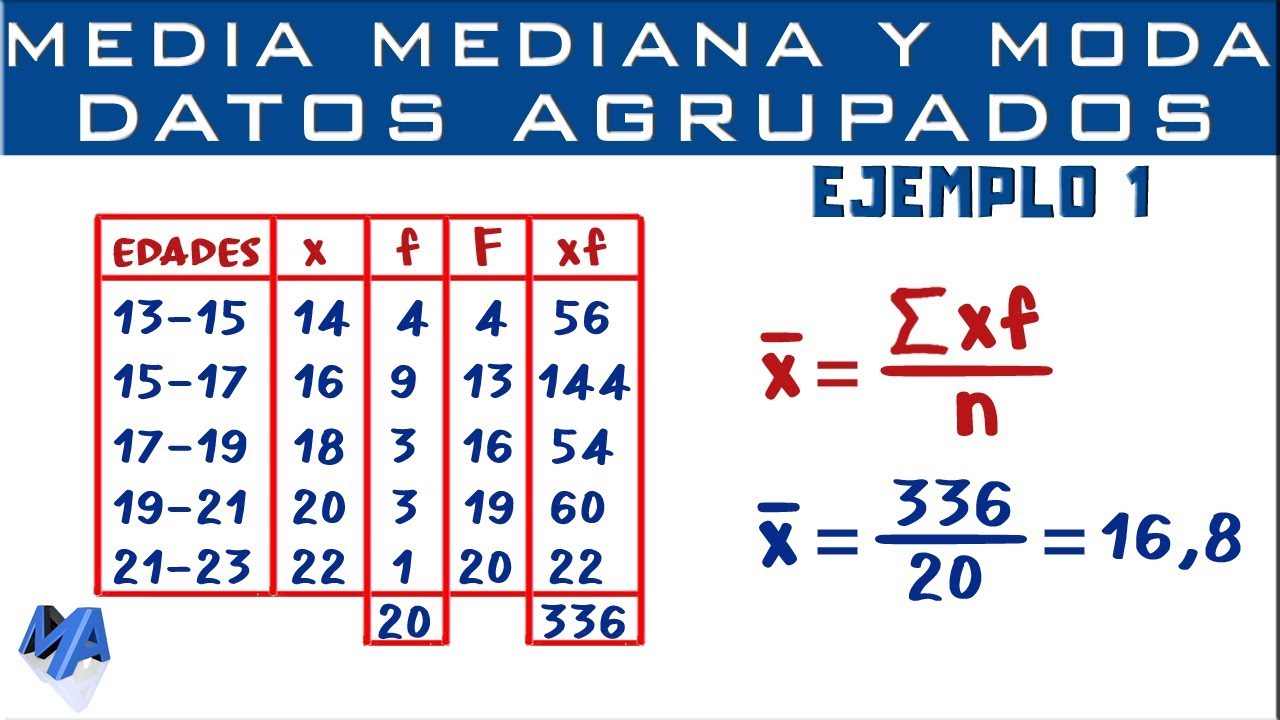
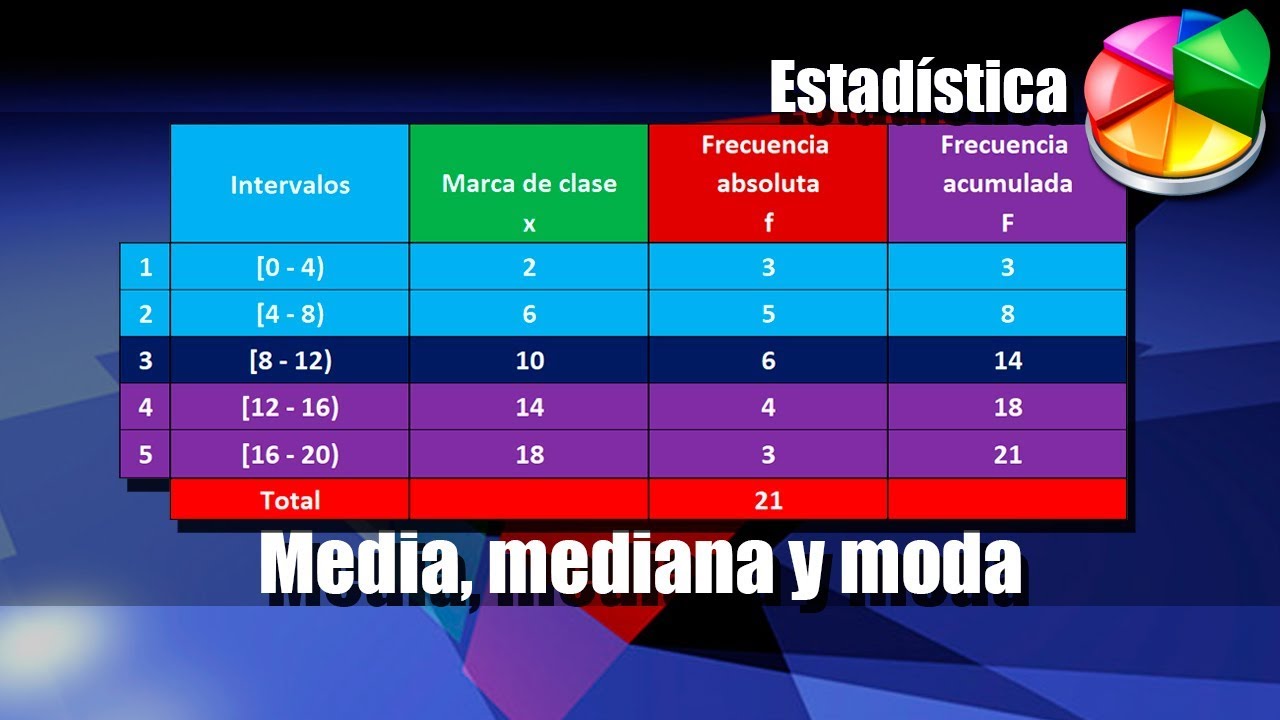
Media, Mediana y Moda para datos agrupados puntualmente
Summary
TLDREn este video, se explica cómo calcular la media, mediana y moda para un conjunto de datos agrupados, utilizando como ejemplo las edades de 60 estudiantes. Se detalla el proceso para encontrar cada una de estas medidas de tendencia central: la media se obtiene con la fórmula de suma de productos entre los valores y sus frecuencias dividida por el número total de datos; la mediana se busca según la posición en la frecuencia acumulada; y la moda es el valor más repetido en el conjunto de datos. Además, se deja un ejercicio práctico para reforzar los conceptos.
Takeaways
- 😀 La media se calcula sumando el producto de cada valor por su frecuencia y dividiendo entre el número total de datos.
- 😀 La mediana es el valor que ocupa la posición central de un conjunto de datos ordenado. Para datos agrupados, se usa la frecuencia acumulada.
- 😀 La moda es el valor que más se repite en un conjunto de datos, es decir, el valor con la frecuencia más alta.
- 😀 Para calcular la media, se debe llenar la casilla de 'x por f' multiplicando cada valor por su frecuencia correspondiente.
- 😀 El total de los datos (N) se obtiene sumando las frecuencias, y siempre debe coincidir con el número de elementos en el conjunto de datos.
- 😀 La posición de la mediana se calcula dividiendo el número total de datos entre 2. En este caso, con 60 estudiantes, la posición es 30.
- 😀 Para encontrar la mediana, se busca la frecuencia acumulada que incluya la posición de la mediana. Si no es exacta, se toma la clase correspondiente.
- 😀 La moda se encuentra buscando la frecuencia máxima en la tabla de frecuencias. El valor de la moda es el que corresponde a esa frecuencia máxima.
- 😀 La frecuencia acumulada se calcula sumando las frecuencias de cada clase hasta llegar al total de datos.
- 😀 En el ejemplo dado, la media, la mediana y la moda de las edades de los estudiantes son 15.26 años, 15 años y 15 años respectivamente.
- 😀 Es importante no confundirse entre la posición de la mediana o la moda y los valores de las frecuencias acumuladas o máximas.
Q & A
¿Cómo se calcula la media de un conjunto de datos agrupados?
-La media se calcula sumando el producto de cada valor de datos (x) por su frecuencia (f), luego se divide entre el número total de datos (n). La fórmula es: Media = (Σ(x * f)) / n.
¿Qué significa la suma de las frecuencias (Σf) en el cálculo de la media?
-La suma de las frecuencias (Σf) representa el número total de datos en el conjunto, es decir, el total de estudiantes o elementos que se están analizando.
¿Cómo se encuentra la mediana en un conjunto de datos agrupados?
-La mediana se encuentra primero calculando la posición de la mediana, dividiendo el número total de datos (n) entre 2. Luego, se busca la frecuencia acumulada que contiene esa posición y se identifica el valor correspondiente en esa clase.
¿Qué es la frecuencia acumulada en el cálculo de la mediana?
-La frecuencia acumulada es el total acumulado de frecuencias a medida que se avanza a través de los intervalos de datos. Es importante para identificar en qué intervalo se encuentra la posición de la mediana.
¿Cómo se determina la moda en un conjunto de datos agrupados?
-La moda se determina identificando el valor de datos (x) que tiene la mayor frecuencia (f). Es el dato que más veces se repite en el conjunto de datos.
Si la frecuencia máxima no corresponde a un dato en específico, ¿cómo se identifica la moda?
-Si hay una frecuencia máxima compartida por más de un valor, el conjunto de datos es multimodal, lo que significa que tiene más de una moda.
¿Por qué es importante acumular las frecuencias cuando se calcula la mediana?
-Es importante acumular las frecuencias porque la mediana se basa en la posición dentro del conjunto de datos ordenado. La frecuencia acumulada permite identificar en qué intervalo se encuentra esta posición.
En el ejemplo con 60 estudiantes, ¿cuál es el promedio de las edades?
-El promedio de las edades es 15,26 años, obtenido dividiendo la suma de las multiplicaciones de las edades por las frecuencias (916) entre el número total de estudiantes (60).
¿Cuál es la diferencia entre la media, la mediana y la moda?
-La media es el promedio de todos los datos, la mediana es el valor central cuando los datos están ordenados, y la moda es el dato que más veces se repite en el conjunto.
En el ejercicio final con los hermanos, ¿cómo se calculó la mediana?
-La mediana se calculó encontrando la posición de la mediana, que corresponde al número 25 al dividir el total de datos (50) entre 2. Luego, se buscó la frecuencia acumulada correspondiente a esa posición y se determinó que la mediana es 2.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)