Menentukan Volume Benda Putar dengan Menggunakan Integral (Integral Part 5) M4THLAB
Summary
TLDRIn this video, Demian Dayani explains how to determine the volume of a solid of revolution using integrals. The video covers two main methods: finding the volume of solids formed by rotating curves around the x-axis and the y-axis. Demian walks through detailed examples, including curves like y = 4 - x² and y = x², as well as more complex shapes like the intersection of a circle and parabola. Through clear explanations and step-by-step calculations, viewers learn how to apply integration to calculate the volumes of rotated regions, ensuring a deeper understanding of the concept.
Takeaways
- 😀 The video focuses on explaining how to calculate the volume of solids formed by rotating curves around the x-axis and y-axis using integrals.
- 😀 The first method discussed involves rotating a curve around the x-axis. The volume is found by squaring the function and integrating with respect to x, multiplied by pi.
- 😀 The second method involves rotating a curve around the y-axis. In this case, the volume is calculated by squaring the function in terms of y and using the same integration process with respect to y.
- 😀 The first example demonstrates finding the volume of a shape formed by rotating the curve y = 4 - x² around the x-axis. The volume is calculated by using definite integrals from 0 to 2.
- 😀 In the first example, the function is squared and integrated, then evaluated using the boundaries to find the exact volume.
- 😀 The second example involves rotating the area between the curves y = x² and y = 2x around the x-axis. The volume is determined by subtracting the lower curve from the upper one and applying the same method as the first example.
- 😀 The second example shows how to calculate the volume formed between two curves by integrating the difference between the squared functions and multiplying by pi.
- 😀 The third example introduces a more complex case where a region bounded by a parabola x = 2√3y² and a circle x² + y² = 1 is rotated around the y-axis. This requires finding the points of intersection between the two shapes to determine integration limits.
- 😀 In the third example, the volume is split into two parts: one for the parabola and one for the circle. Each part requires a separate integral with respect to y.
- 😀 The video emphasizes the importance of understanding integral calculus when dealing with volumes of revolution and shows multiple examples to help viewers grasp the concept.
Q & A
What is the main topic of the video?
-The main topic of the video is about determining the volume of a solid formed by rotating a curve around an axis using definite integrals.
How is volume determined when a curve is rotated around the x-axis?
-When a curve is rotated around the x-axis, the volume is determined using the formula: Volume = π * integral from a to b of [f(x)]^2 dx. This involves squaring the curve and multiplying by π.
What is the key difference between calculating area and volume in the examples provided?
-The key difference is that while calculating area, we consider the curve directly, for volume, we square the curve before integrating.
What method is used to find the volume when a curve is rotated around the y-axis?
-When a curve is rotated around the y-axis, the volume is calculated using the formula: Volume = π * integral from a to b of [f(y)]^2 dy, where the curve is expressed in terms of y.
What does the function y = 4 - x^2 represent in the first example?
-The function y = 4 - x^2 represents a parabola that opens downward, and the volume formed by rotating this curve around the x-axis is being calculated.
What is the process to find the points where the curve y = 4 - x^2 intersects the x-axis?
-To find the points of intersection with the x-axis, set y = 0 and solve the equation 4 - x^2 = 0, which gives the points x = -2 and x = 2.
In the second example, what curves are being rotated, and what is the resulting volume?
-In the second example, the curves y = x^2 and y = 2x are rotated around the x-axis. The volume formed is calculated by subtracting the volume under the curve y = x^2 from the volume under the curve y = 2x and multiplying by π.
How do you calculate the volume in the case of two curves, y = x^2 and y = 2x, when rotated around the x-axis?
-The volume is calculated by subtracting the integral of (x^2)^2 from (2x)^2, and multiplying the result by π. The limits of integration are from x = 0 to x = 2.
What is the significance of squaring the functions before integrating them in the volume calculation?
-Squaring the functions before integrating is essential because the volume of a solid of revolution is proportional to the square of the distance from the axis of rotation.
What is the geometric interpretation of the volume formula used in the video?
-The geometric interpretation is that the volume of a solid of revolution can be thought of as the sum of infinitely thin cylindrical slices, where the area of each slice is the square of the radius (the function value) times π.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

KALKULUS | APLIKASI INTEGRAL | VOLUME BENDA PUTAR

Volume: Lempeng, Cakram, Cincin | Aplikasi Integral (Part 2) | Kalkulus
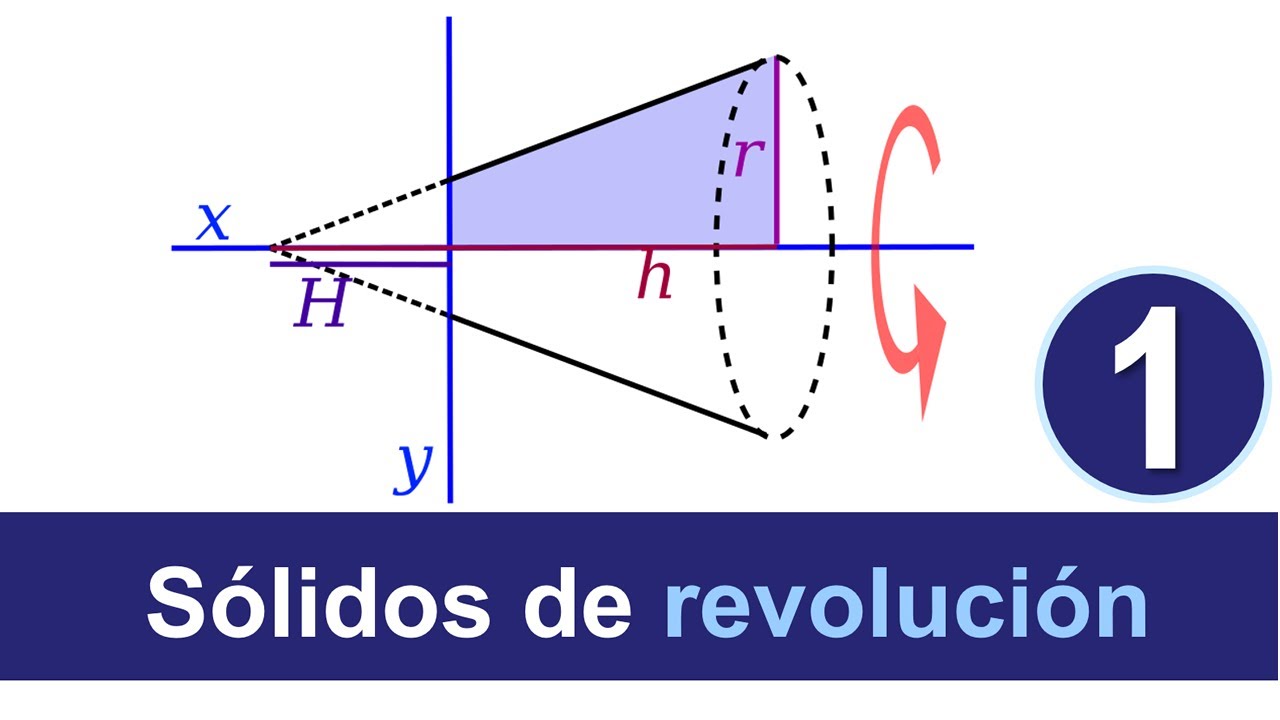
Cálculo Integral - Volumen de sólidos de revolución #1
Integrales dobles 2

UNIDAD 3: Integrales dobles en coordenadas rectangulares - Volumen de un sólido

Integrals: Crash Course Physics #3
5.0 / 5 (0 votes)