KALKULUS | APLIKASI INTEGRAL | VOLUME BENDA PUTAR

Summary

This video explains two methods for calculating the volume of solids of revolution using integral calculus: the disk method and the washer method. The disk method is used when a region is rotated around an axis, forming a solid like stacked disks, with the volume formula involving the square of the function’s radius. The washer method is applied when there’s a hole in the middle of the solid, using two functions to calculate the outer and inner radii. Through detailed examples, the video demonstrates how to set up and solve the integrals for both methods, helping viewers understand how to calculate volumes in various scenarios.

Takeaways

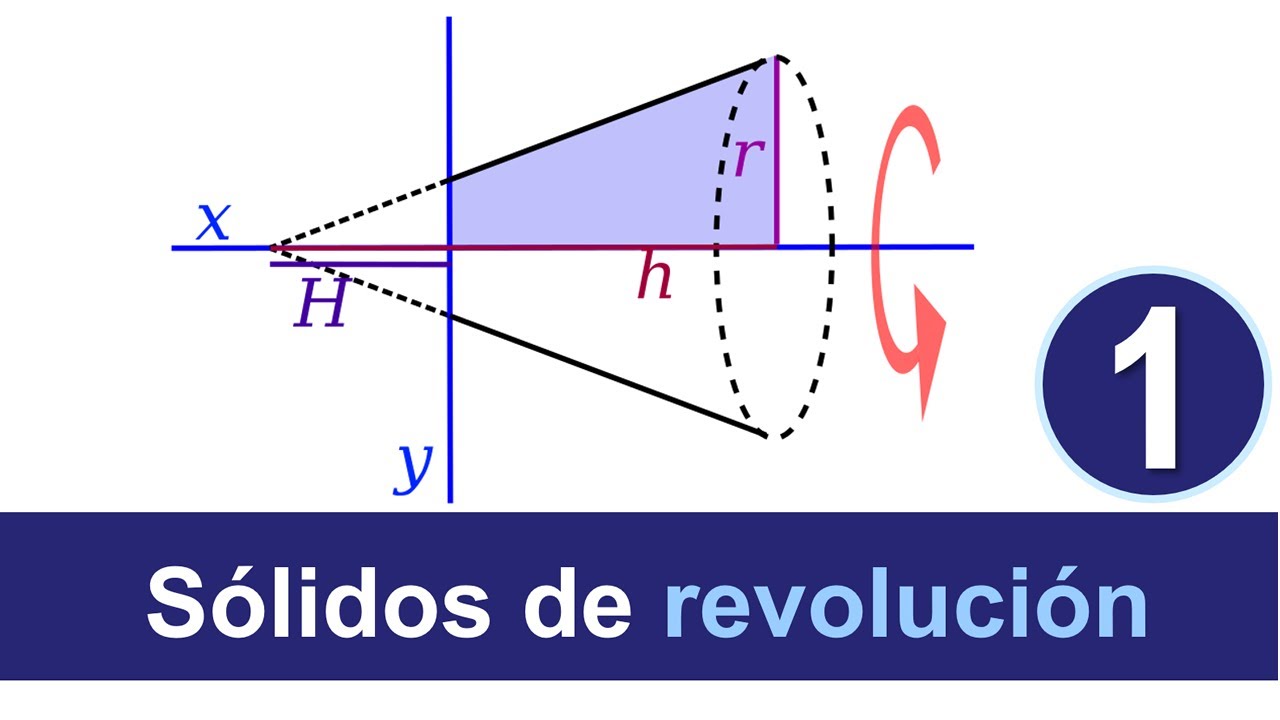
• 😀 The disk method calculates the volume of a solid of revolution formed by rotating a region around the x-axis using vertical slices.
• 😀 The washer method calculates the volume of a solid of revolution with a hollow center by revolving a region between two curves around the x-axis.
• 😀 In the disk method, the volume is calculated by squaring the radius of the function and integrating with respect to the x-axis.
• 😀 For solids of revolution created by rotating regions around the y-axis, the disk method uses horizontal slices instead of vertical slices.
• 😀 To calculate volume with the disk method, use the formula V = π ∫ (f(x))² dx, where f(x) is the function representing the boundary of the region.
• 😀 When using the washer method, the volume is found by subtracting the inner radius squared from the outer radius squared and integrating.
• 😀 The volume formula for the washer method is V = π ∫ [(f(x))² - (g(x))²] dx, where f(x) and g(x) represent the outer and inner curves, respectively.
• 😀 The integral of a function with limits is used to find the exact volume, and partitioning the area into infinitesimally small slices helps to approximate this volume.
• 😀 The script provides examples using both the disk and washer methods, including specific regions like y = x², y = 4, and lines such as x = 2.
• 😀 The final answer for each problem is obtained after performing integration and substituting the appropriate limits to find the volume of the solid formed.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.