Volume: Lempeng, Cakram, Cincin | Aplikasi Integral (Part 2) | Kalkulus

Summary

This video delves into the application of integrals to calculate the volume of solid objects, particularly focusing on the methods of plates, discs, and rings. The speaker illustrates the concept by solving an example where the area bounded by a curve is rotated around the y-axis to form a solid. The discussion explains how to partition the shape into small discs or rings, calculate the volume of each partition, and then integrate to find the total volume. The video also contrasts the full solid with hollow shapes, offering an engaging exploration of integral applications in geometry.

Takeaways

• 😀 The video introduces the concept of using integrals to calculate the volume of solids formed by rotating an area around the y-axis.
• 😀 It explains the method of using plates, discs, and rings to partition the solid object and calculate its volume.
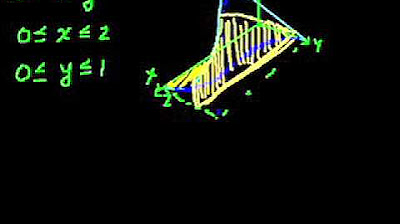
• 😀 The first example involves rotating the area bounded by the curve y = 4 - x², the x-axis, and the y-axis to create a solid dome shape.
• 😀 The volume is calculated by slicing the solid into discs, with each disc's volume determined by the formula πr²Δy, where the radius is determined by the curve equation.
• 😀 The process involves setting up an integral for the volume calculation, which is then evaluated to find the solid's total volume.
• 😀 The video then introduces a more challenging example, where the solid has a hollow interior, resembling a torus or donut shape.
• 😀 To calculate the volume of a hollow solid, the volume of the outer cylinder is subtracted by the volume of the inner cylinder.
• 😀 The outer radius is given by the curve y = 4 - x², while the inner radius is defined by another equation y = -2x + 4.
• 😀 The video explains the use of integrals to calculate the volume of this hollow shape, using the formula for the difference of two cylinders.
• 😀 The final volume of the hollow solid is calculated by subtracting the volume of the cone (the inner part) from the full solid volume.
• 😀 The video concludes by discussing how integrals can be used to calculate the volume of different solid shapes formed by rotating areas around axes, either the x-axis or y-axis.

Q & A

What is the main topic discussed in the video?

The main topic is using integrals to calculate the volume of solids formed by rotating areas bounded by curves, specifically using the disk, washer, and ring methods.

What does the curve y = 4 - x² represent in the context of the problem?

The curve y = 4 - x² represents a parabolic shape that is bounded by the x-axis and the y-axis. This area is rotated about the y-axis to form a solid object.

What is the method used to calculate the volume of the solid formed by rotating the area about the y-axis?

The volume is calculated using the disk method, where the area is divided into small cylindrical discs, each with a small height (Δy) and a varying radius.

How is the volume of each cylindrical disc calculated?

The volume of each cylindrical disc is calculated by multiplying the cross-sectional area of the disc (πx²) by its height (Δy).

What is the integral setup to find the volume of the solid formed by rotation?

The integral setup involves integrating π(4 - y) from y = 0 to y = 4, resulting in the volume of the solid.

How is the volume formula for the first solid derived?

The volume is derived by performing the integration of the area formula, π(4 - y)², from 0 to 4. After performing the integration, the result is 8 cubic units.

What is the difference when the shape has a hollow center?

When the shape has a hollow center, the volume calculation involves subtracting the volume of the inner solid (cone) from the outer solid's volume, creating a ring-shaped volume.

How is the volume of the hollow solid calculated?

The volume of the hollow solid is calculated by subtracting the volume of the inner cylinder (cone) from the volume of the outer cylinder. The formula involves subtracting the area of the inner cylinder from the outer cylinder at each height level.

What does the second integral calculate in the case of the hollow solid?

The second integral calculates the volume of the hollow solid by subtracting the inner radius's volume from the outer radius's volume, resulting in a ring-shaped volume.

How does the volume of the cone factor into the hollow solid's volume?

The volume of the cone is subtracted from the volume of the full solid to account for the hollow center. The cone’s volume is calculated as one-third of the base area times the height.