Integrals: Crash Course Physics #3
Summary
TLDRIn this episode, the concept of integrals in calculus is introduced as the inverse of derivatives, focusing on their role in physics. The video explains how integrals help determine displacement, velocity, and acceleration by finding the area under curves on a graph. Using the example of a falling tennis ball, the script demonstrates how to calculate position and velocity through integration, addressing the challenges of constants and initial values. The episode covers essential shortcuts for finding integrals, showcasing practical applications in understanding motion and setting the stage for more advanced calculus concepts.
Takeaways
- 😀 Derivatives describe how an equation is changing, while integrals help determine the area under a curve, representing total change in position or other quantities.
- 😀 Integrals are the inverse of derivatives, and they can be used to calculate quantities such as velocity and position from acceleration.
- 😀 In the context of motion, velocity is the integral of acceleration, and position is the integral of velocity.
- 😀 To find the integral, the area under the curve of a function is broken down into infinitely small rectangles, and the sum of their areas gives the integral.
- 😀 The power rule for derivatives can be reversed for integrals: you add one to the exponent and divide by the new exponent.
- 😀 Constants in equations can create multiple possible integrals, as the derivative of a constant is zero, resulting in infinite possible equations with the same derivative.
- 😀 To represent all possible integrals, mathematicians use a constant 'C' at the end of the integral, which accounts for all the potential values.
- 😀 If an initial value, such as the starting position or velocity, is known, the constant 'C' can be determined, and the integral can be uniquely defined.
- 😀 An example of using integrals involves calculating the height of a bedroom window by analyzing the fall of a ball, with known acceleration and time.
- 😀 Using kinematic equations and integrals, the velocity and position of a falling object can be calculated, incorporating initial conditions like starting velocity and position.
Q & A
What is the main topic discussed in this episode of Crash Course Physics?
-The main topic discussed in this episode is integrals, particularly how they are used in calculus to find the area under a curve and describe motion, including position and velocity.
How are integrals related to derivatives?
-Integrals are the inverse of derivatives. While derivatives tell us how an equation changes, integrals help us find the total accumulation of changes, such as the area under a curve.
What does the integral of acceleration represent?
-The integral of acceleration gives the velocity of an object, as velocity is the accumulated change in position over time.
Why are constants important in integrals?
-Constants are important because they represent an infinite number of possible integrals that all share the same derivative. The constant 'C' is added to the integral to account for all these possibilities.
What is the significance of the constant 'C' in integrals?
-The constant 'C' represents all possible vertical shifts of the integral's graph, accounting for different initial conditions. It is used when the exact value of the integral's starting point is unknown.
How do initial values help in determining the value of 'C'?
-Initial values, such as the initial velocity or position, help determine the exact starting point of the graph. By using initial conditions, the constant 'C' can be calculated, making the integral more specific.
What is the process for finding an integral of a function?
-To find an integral, you reverse the process of differentiation. For example, to find the integral of 2t, you would use the power rule by adding one to the exponent and dividing by the new exponent.
How does the power rule work in reverse for integrals?
-The power rule for integrals works by adding one to the exponent and then dividing the variable by the new exponent. For example, the integral of t^n is (t^(n+1))/(n+1).
What is the role of the displacement curve in this episode?
-The displacement curve equation is derived by integrating acceleration twice: first to find velocity, and then to find position. It represents how an object's position changes over time given its initial velocity and acceleration.
How does knowing the acceleration and time help in determining the height of an object?
-By integrating the acceleration over time, you can find the velocity. A second integration gives you the position, and using the time it takes for the object to fall, you can calculate the height of the object (e.g., the height of the bedroom window).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

BELAJAR INTEGRAL DARI DASAR DALAM 12 MENIT!

Derivatives: Crash Course Physics #2

KALKULUS | INTEGRAL | INTEGRAL TAK TENTU (ANTI TURUNAN)

Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
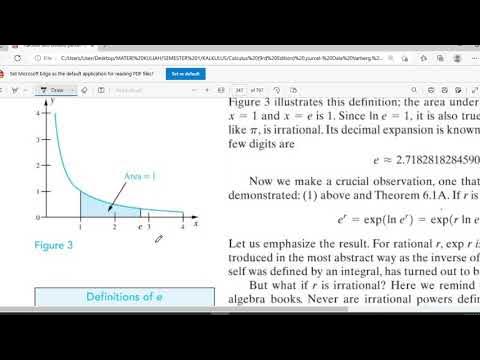
Fungsi Transenden 3 (Fungsi Eksponensial Natural)

Calculus AB/BC – 6.7 The Fundamental Theorem of Calculus and Definite Integrals
5.0 / 5 (0 votes)