Logarithms - Real Life Applications | Logs | Don't Memorise
Summary
TLDRThis video explains the concept of logarithms, focusing on logarithms to the base 10 and their real-life applications. It demonstrates how to solve logarithmic equations, such as log(100) and log(1000), and explains the significance of these numbers in everyday contexts, like salary or the distance from Earth to the Sun. The video also explores how logarithmic scales, like the Richter scale for earthquakes, help to represent vast variations in values in a manageable way. The key takeaway is how logarithms simplify complex measurements and allow us to visualize extreme differences more easily.
Takeaways
- 😀 Logarithms help us find the exponent to which a base must be raised to produce a given number (e.g., log base 10 of 100 is 2, since 10^2 = 100).
- 😀 The logarithmic scale is used to simplify large numerical differences, making them easier to compare and plot on a number line.
- 😀 In logarithmic form, log(1) to the base 10 equals 0 because 10^0 = 1.
- 😀 The log of 10 to the base 10 is 1, since 10^1 = 10.
- 😀 By converting numbers into their logarithmic equivalents, we can manage very large or small numbers more effectively on a number line.
- 😀 The Richter scale, used to measure earthquake magnitudes, is based on a logarithmic scale (base 10).
- 😀 Each whole number increase on the Richter scale represents a tenfold increase in the energy released by an earthquake.
- 😀 A magnitude 7.0 earthquake on the Richter scale is 10 times stronger than a 6.0, and a 9.0 earthquake is 1000 times stronger than a 6.0.
- 😀 Logarithmic scales like the Richter scale allow for easier comparison of events with drastic differences in magnitude.
- 😀 Logarithms are crucial for expressing and understanding values that vary greatly, such as the distance from Earth to the Sun or the number of cells in the human body.
- 😀 The use of logarithms in real-world applications helps us navigate and make sense of data that spans vast ranges, from tiny to enormous.
Q & A
What is a logarithm and how is it represented in exponential form?
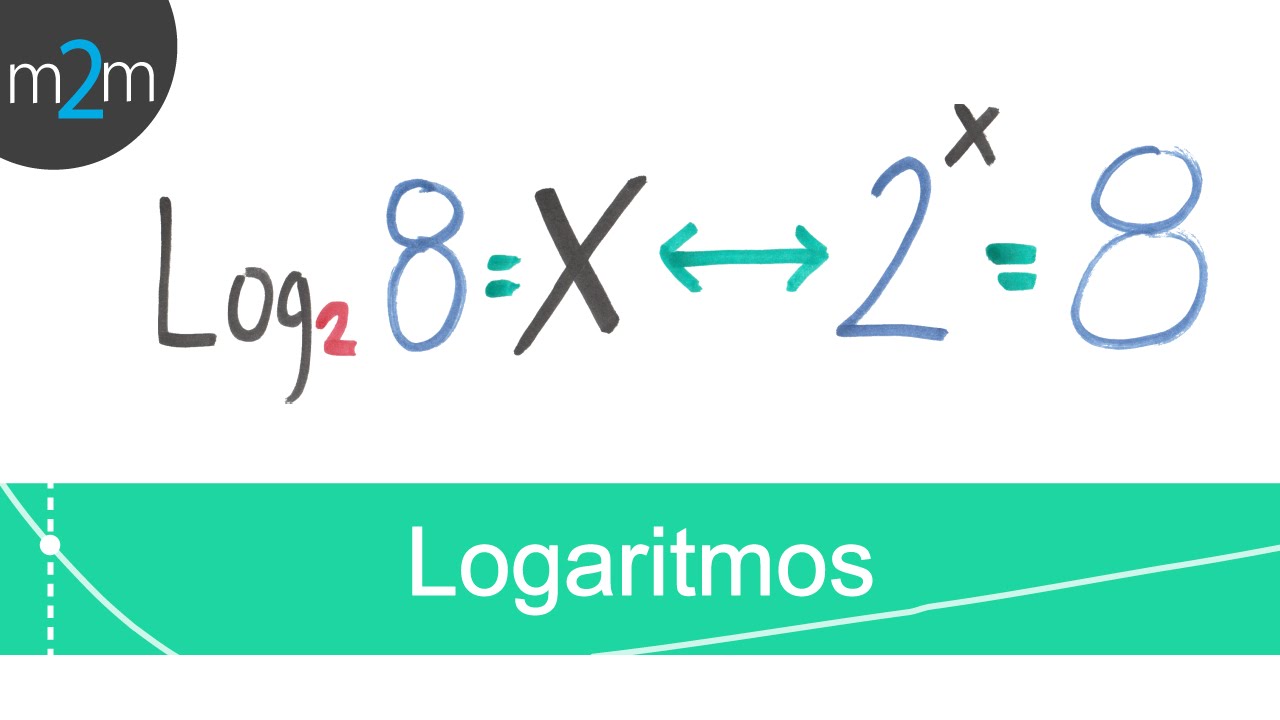
-A logarithm is the inverse of exponentiation. It represents the power to which a base must be raised to produce a given number. In exponential form, log_b(a) = x means that b^x = a, where b is the base and x is the exponent.
What is the value of log₁₀(100) and how do you calculate it?
-The value of log₁₀(100) is 2, because 10 raised to the power of 2 equals 100 (10^2 = 100).
How can logarithms help in simplifying the representation of large numbers?
-Logarithms help by converting large numbers into smaller, more manageable values. Instead of dealing with a wide range of numbers, taking the logarithm allows us to represent them on a compressed scale, making comparisons easier.
Why do logarithmic scales work well for plotting large numbers like 1,000, 10,000, and 1,000,000?
-Logarithmic scales convert large numbers into smaller values, making them easier to fit on a number line. For example, log₁₀(1,000) = 3, log₁₀(10,000) = 4, and log₁₀(1,000,000) = 6, which helps in visualizing and comparing numbers that span wide ranges.
What is the relationship between logarithms and the Richter scale?
-The Richter scale uses a logarithmic scale to measure earthquake magnitudes. Each increase by one unit on the scale represents a tenfold increase in the earthquake's strength.
How is the Richter scale a logarithmic scale, and what does this mean for earthquake measurements?
-The Richter scale is a base-10 logarithmic scale, meaning that an earthquake with a magnitude of 7.0 is 10 times stronger than one with a magnitude of 6.0. A magnitude 9.0 earthquake is 100 times stronger than a 7.0, highlighting how logarithms scale massive differences in intensity.
How do logarithms help in narrowing down large variations in real-world data?
-Logarithms help by compressing large variations into a manageable scale, allowing for easier comparisons. For example, logarithmic scales can be used to understand differences in salary, population size, or earthquake strength.
What is the significance of using logarithms in real-life scenarios like measuring earthquakes?
-Logarithms provide a practical way to measure phenomena with large variations, such as earthquakes. Without logarithms, it would be difficult to represent the vast difference in earthquake magnitudes on a simple scale.
Can you explain how the logarithm of 1,000 to the base 10 works?
-log₁₀(1,000) equals 3 because 10 raised to the power of 3 equals 1,000 (10^3 = 1,000).
How does the base of a logarithm (in this case, 10) affect the result?
-The base of a logarithm determines the scale of the logarithmic function. In base-10 logarithms, the result tells us how many times 10 must be multiplied by itself to reach the number in question. For example, log₁₀(1,000) equals 3 because 10^3 = 1,000.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)