* Distancia entre un punto y una recta (PARTE 1)
Summary
TLDREn este video, se explica cómo calcular la distancia mínima entre un punto y una recta utilizando la fórmula de distancia perpendicular. A través de un ejemplo práctico, se demuestra cómo aplicar la fórmula, que involucra los coeficientes de la recta y las coordenadas del punto. Además, se describe el proceso de graficar tanto el punto como la recta en un plano cartesiano, mostrando cómo encontrar los puntos de intersección con los ejes. El resultado obtenido, la distancia mínima, es de aproximadamente 3.32 unidades, lo que ilustra cómo se interpreta y aplica este cálculo en problemas geométricos.
Takeaways
- 😀 La fórmula para calcular la distancia mínima entre un punto y una recta es: |Ax + By + C| / √(A² + B²).
- 😀 El valor absoluto es fundamental en la fórmula para evitar distancias negativas, ya que las distancias no pueden ser negativas.
- 😀 Para aplicar la fórmula, es necesario tener la ecuación de la recta en su forma general: Ax + By + C = 0.
- 😀 Al sustituir los valores del punto en la fórmula, se obtiene el resultado de la distancia entre el punto y la recta.
- 😀 En el ejercicio específico, se sustituye un punto A(4, 3) y la ecuación de la recta 3x + 2y - 6 = 0.
- 😀 Al resolver la sustitución, la distancia calculada entre el punto y la recta es aproximadamente 3.32 unidades.
- 😀 Es importante recordar que la distancia entre un punto y una recta se mide de forma perpendicular.
- 😀 Para graficar la recta, se pueden usar los interceptos en los ejes X y Y, obteniendo los puntos (0, 3) y (2, 0).
- 😀 Se recomienda visualizar la distancia mediante la gráfica para comprender mejor el concepto geométrico de la distancia mínima.
- 😀 Al graficar el punto y la recta, se confirma que la distancia perpendicular desde el punto a la recta es 3.32.
- 😀 La práctica de graficar y calcular distancias permite tener una comprensión más clara de cómo se relacionan puntos y rectas en el plano.
Q & A
¿Cómo se calcula la distancia mínima entre un punto y una recta?
-La distancia mínima se calcula utilizando la fórmula del valor absoluto de la ecuación de la recta general, que se divide por la raíz cuadrada de la suma de los cuadrados de los coeficientes de la recta.
¿Qué significa que la distancia mínima entre el punto y la recta sea la perpendicular?
-La distancia mínima es la más corta entre el punto y la recta, y se encuentra a lo largo de una línea perpendicular desde el punto hasta la recta.
¿Cómo se debe escribir la ecuación de la recta para aplicar la fórmula de distancia?
-La ecuación de la recta debe estar en su forma general, es decir, como Ax + By + C = 0, donde A, B y C son constantes.
¿Qué valores deben sustituirse en la fórmula para calcular la distancia?
-Se deben sustituir los valores de las coordenadas del punto (x, y) en la fórmula, así como los coeficientes A y B de la ecuación de la recta.
¿Qué sucede con el valor absoluto en la fórmula de distancia?
-El valor absoluto asegura que la distancia sea siempre positiva, ya que las distancias no pueden ser negativas.
¿Cómo se obtiene el valor de la distancia después de sustituir los valores en la fórmula?
-Se realiza la multiplicación y simplificación según la fórmula, y luego se divide el resultado por la raíz cuadrada de la suma de los cuadrados de los coeficientes A y B.
¿Qué se debe hacer si el valor de la distancia es negativo?
-Si el valor de la distancia es negativo, se debe convertir en positivo, ya que las distancias no tienen signo negativo.
¿Qué significa que el resultado final sea 3.32 en el ejemplo del cálculo de la distancia?
-El resultado 3.32 es la distancia mínima entre el punto y la recta, calculada mediante la fórmula y la sustitución de valores en el ejemplo.
¿Cómo se puede graficar el punto y la recta en el plano cartesiano?
-Para graficar el punto, se ubica su coordenada (x, y) en el plano cartesiano. Para graficar la recta, se encuentran sus intersecciones con los ejes X y Y, y se traza una línea entre estos puntos.
¿Cómo se encuentran los puntos de intersección de la recta con los ejes?
-Para encontrar el punto de intersección con el eje Y, se sustituye x = 0 en la ecuación de la recta y se resuelve para y. Para encontrar la intersección con el eje X, se sustituye y = 0 en la ecuación y se resuelve para x.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

29. Distancia entre dos rectas

1. Distancia entre dos puntos. Deducción de la fórmula y ejemplos

Distancia entre dos puntos Ejemplo 1

Mod. 5 - 20 Conversión de coordenadas a distancias

Definición y fórmula para la distancia en la Geometría del Taxista, Todos los Niveles
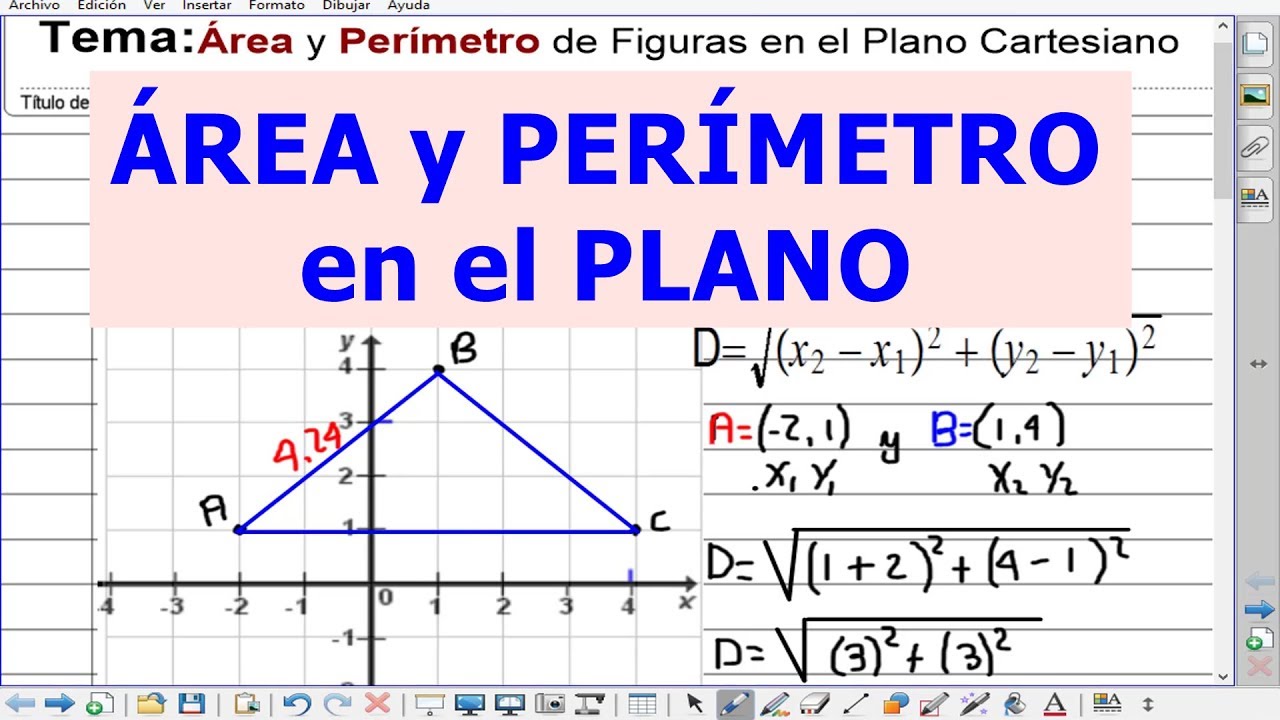
Área y Perímetro de Figuras en el Plano Cartesiano.
5.0 / 5 (0 votes)
