Ec. de circunferencia, dado centro y radio│fuera origen
Summary
TLDREl video enseña cómo obtener la ecuación ordinaria y la gráfica de una circunferencia a partir de su centro y radio. Se presentan varios ejemplos, comenzando con un centro en (1,3) y radio 4, y se demuestra cómo sustituir estos valores en la fórmula de la circunferencia. Se exploran también otros centros y radios, incluyendo valores negativos y fraccionarios, enfatizando la importancia de representar gráficamente las circunferencias correctamente. La explicación es clara y detalla el proceso paso a paso, haciendo accesible el concepto de circunferencias a los espectadores.
Takeaways
- 😀 Se explica cómo obtener la ecuación ordinaria de una circunferencia dado su centro y radio.
- 😀 La ecuación de la circunferencia se basa en el formato (x - h)² + (y - k)² = r², donde (h, k) es el centro.
- 😀 Un ejemplo muestra el centro en (1, 3) y radio 4, lo que da como resultado la ecuación (x - 1)² + (y - 3)² = 16.
- 😀 Para graficar una circunferencia, se debe identificar el centro y luego utilizar el radio para determinar los puntos alrededor del centro.
- 😀 En el segundo ejemplo, con centro en (-1, 5) y radio 1, se encuentra la ecuación (x + 1)² + (y - 5)² = 1.
- 😀 La importancia de utilizar fracciones para mayor precisión en los cálculos se enfatiza en el manejo de radios y coordenadas.
- 😀 El tercer ejercicio presenta un centro en (0, -7) y un radio de 5, resultando en la ecuación x² + (y + 7)² = 25.
- 😀 Se discute la equivalencia entre usar fracciones y decimales al expresar radios en la ecuación.
- 😀 Se recalca que, al graficar, es útil tener un compás para facilitar la representación de la circunferencia.
- 😀 Se concluye que, con el centro y el radio, se puede encontrar fácilmente la ecuación y graficar la circunferencia de manera efectiva.
Q & A
¿Cuál es la ecuación estándar de una circunferencia?
-La ecuación estándar de una circunferencia con centro en (h, k) y radio r es (x - h)² + (y - k)² = r².
¿Cómo se determina la ecuación de una circunferencia si el centro está en (1, 3) y el radio es 4?
-Sustituyendo los valores en la ecuación, obtenemos (x - 1)² + (y - 3)² = 16.
¿Qué pasos se siguen para graficar una circunferencia?
-Primero se ubica el centro, luego se mide el radio en todas direcciones y se trazan puntos, finalmente se unen esos puntos para formar la circunferencia.
¿Qué sucede con el signo al sustituir el valor del centro en la ecuación?
-El signo se invierte: si el centro es (h, k), se usa (x - h) y (y - k) en la ecuación.
¿Cómo se simplifica la ecuación de una circunferencia con centro en (-1, 5) y radio 1?
-La ecuación resultante es (x + 1)² + (y - 5)² = 1.
¿Cuál es la diferencia entre usar fracciones y decimales en la ecuación de una circunferencia?
-Las fracciones son más exactas, pero los decimales pueden ser más fáciles de trabajar en algunos casos.
Al graficar, ¿cómo se determina la posición del centro si sus coordenadas son fraccionarias?
-Se ubica el centro en el plano cartesiano de acuerdo a sus coordenadas fraccionarias y se mide el radio desde ese punto.
¿Qué ecuación se obtiene para una circunferencia con centro en (0, -7) y radio 5?
-La ecuación es x² + (y + 7)² = 25.
Si el centro es (-3/4, -7/3) y el radio es 1/2, ¿cuál es la ecuación de la circunferencia?
-La ecuación es (x + 3/4)² + (y + 7/3)² = 1/4.
¿Por qué es importante entender cómo graficar una circunferencia?
-Es fundamental para visualizar conceptos matemáticos y aplicar la teoría de coordenadas en problemas prácticos.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Circunferencias: De general a ordinaria | Matemáticas | Khan Academy en Español
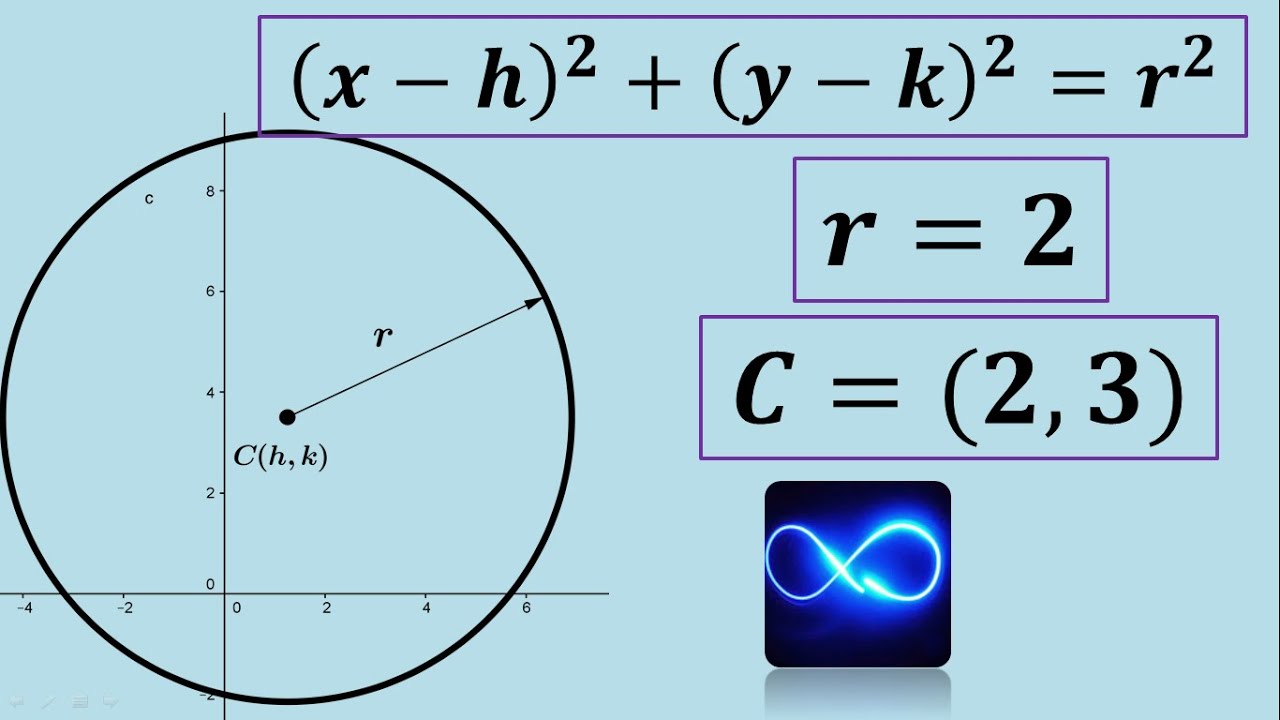
Ordinary and general equation of circumference with given center and radius (Example 1)

Find center and radius of circumference (completing perfect square trinomial)

CIRCUNFERENCIA: De la ecuación General a la Ordinaria. FÁCIL. 2 ejemplos

Ecuación de la circunferencia con centro fuera del origen (tercera parte).

Ecuación de la circunferencia con centro fuera del origen (cuarta parte)
5.0 / 5 (0 votes)
