Incompletely specified Functions (Dont Care Terms)
Summary
TLDRThis tutorial covers incompletely specified functions, often termed 'don't care' conditions, in digital logic design. It explains the concept of such functions, where not every output is defined for all possible input combinations. The video illustrates how these functions can simplify logic design and enhance efficiency in creating logical circuits. Examples are provided to clarify how to utilize these conditions effectively, facilitating better output generation and optimization of logic systems. Overall, the tutorial serves as a practical guide for understanding and applying 'don't care' functions in various digital applications.
Takeaways
- 😀 Incomplete specifications for functions can lead to undefined outputs for various input combinations.
- 😀 A completely specified function requires an output value to be defined for every possible input combination.
- 😀 Big Boss's scanning of all combinations highlights how certain functions can remain incomplete in their specifications.
- 😀 When input variables are ABCD, some combinations may not yield a defined output value, which complicates the analysis.
- 😀 Understanding the relationship between input combinations and output values is crucial for effective function design.
- 😀 The tutorial emphasizes the importance of logical expressions in defining outputs accurately.
- 😀 Systems that do not care about certain input combinations can be problematic in generating outputs.
- 😀 The role of binary numbers and their representation in logical functions is highlighted in the context of input-output mapping.
- 😀 Different groups of combinations can lead to distinct outputs, demonstrating the significance of groupings in function design.
- 😀 Finally, the tutorial suggests methods for developing logical circuits that can efficiently handle defined and undefined outputs.
Q & A
What are incompletely specified functions?
-Incompletely specified functions are functions where not every possible combination of input variables is defined to produce an output value.
How do incompletely specified functions relate to the concept of 'don't care' conditions?
-'Don't care' conditions refer to situations where certain input combinations do not affect the output, allowing for flexibility in function implementation.
What is a complete specification of a function?
-A complete specification requires that every possible combination of input variables produces a known output value.
Can you give an example of how to handle 'don't care' conditions in logic functions?
-In logic design, 'don't care' conditions can be used to simplify the function, allowing those combinations to be assigned values that help minimize the overall logic circuit.
What is the significance of input combinations in defining functions?
-Input combinations are crucial as they determine the behavior of the function; missing combinations can lead to incompletely defined outputs.
Why is it important to define outputs for every combination of input variables?
-Defining outputs for every input combination ensures that the function operates reliably and predictably in all scenarios.
What tools or methods are used to visualize input-output relationships?
-Truth tables and Karnaugh maps are common tools used to visualize and simplify the relationships between inputs and outputs in digital logic design.
How can the concept of 'don't care' help in circuit optimization?
-'Don't care' conditions provide opportunities to eliminate unnecessary logic gates, leading to a more efficient circuit design.
What challenges arise when working with incompletely specified functions?
-Challenges include ensuring that the function behaves correctly across all defined scenarios and dealing with the potential for ambiguity in outputs.
How do examples like binary numbers apply to the concepts discussed in the script?
-Binary numbers illustrate how input combinations can yield various outputs, and examining them can highlight the importance of complete specifications in logical functions.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
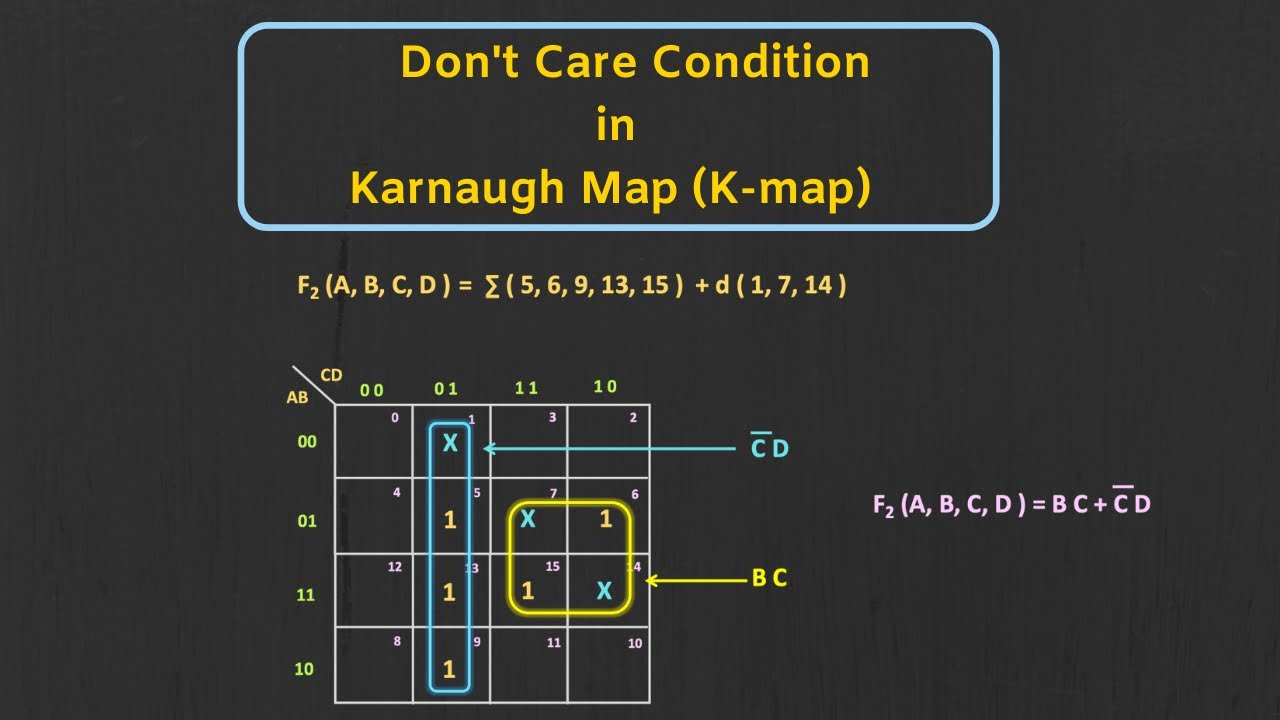
Don't Care Conditions in Karnaugh Map (with Solved Examples)

Logic implementation using Programmable Logic Array (PLA)

Implementation of all logic gates with NAND gate | Design with universal gates | digital electronics

4 Variable K Map | Minimisation of given Function using K Map | By Mathur Sir

Introduction to Programmable Logic Devices (PLDs)

Introduction to Karnaugh Maps - Combinational Logic Circuits, Functions, & Truth Tables
5.0 / 5 (0 votes)