Circunferencias: De general a ordinaria | Matemáticas | Khan Academy en Español
Summary
TLDREste video explica cómo transformar la ecuación general de una circunferencia en su forma ordinaria. A través de cuatro pasos claros, se enseña a agrupar términos, encontrar trinomios cuadrados perfectos, igualar la ecuación y factorizarla. Usando un ejemplo específico, el video demuestra cómo calcular el centro y el radio de la circunferencia a partir de su ecuación general, enfatizando que este proceso no es complicado y que la práctica es fundamental para dominarlo.
Takeaways
- 😀 Un general puede dejar su ejército y, de manera similar, las ecuaciones de circunferencias pueden transformarse entre sí.
- 😀 Para convertir una ecuación general de circunferencia en una ordinaria, se deben seguir ciertos pasos.
- 😀 El primer paso es agrupar y separar los términos de las variables x y y, dejando espacio para los trinomios cuadrados perfectos.
- 😀 El segundo paso consiste en trasladar el término constante al otro lado de la ecuación, convirtiendo una resta en suma.
- 😀 Para formar trinomios cuadrados perfectos, se toma el coeficiente de x o y, se divide entre 2 y se eleva al cuadrado.
- 😀 Se agregan los términos necesarios a la ecuación para completar los trinomios cuadrados perfectos.
- 😀 En el tercer paso, se iguala la ecuación sumando los cuadrados que se incorporaron al lado derecho.
- 😀 La suma de los números resulta en el valor del lado derecho de la ecuación, que será 16 en este caso.
- 😀 El cuarto paso es factorizar cada trinomio cuadrado perfecto, utilizando la raíz cuadrada de los términos.
- 😀 Al final del proceso, se determina que el centro de la circunferencia es (2, 2) y el radio es 4.
Q & A
¿Cuál es el objetivo de transformar una ecuación general de circunferencia a una ecuación ordinaria?
-El objetivo es identificar el centro y el radio de la circunferencia a partir de su ecuación general.
¿Qué forma tiene la ecuación general de la circunferencia que se utiliza en el video?
-La forma de la ecuación general es x² + y² + 4x + 4y - 8 = 0.
¿Cuál es el primer paso para transformar la ecuación de la circunferencia?
-El primer paso es agrupar y separar los términos de las variables x y y, dejando espacio para los trinomios cuadrados perfectos.
¿Qué se hace con el término constante en la ecuación general?
-Se despeja el término constante y se lleva al otro lado de la ecuación, convirtiéndose en una suma.
¿Cómo se encuentra el término faltante para el trinomio cuadrado perfecto de x?
-Se toma el coeficiente de x, se divide entre dos, y se eleva al cuadrado para obtener el término que falta.
¿Qué pasos se siguen para encontrar el trinomio cuadrado perfecto para y?
-Se toma el coeficiente de y, se divide entre dos, y se eleva al cuadrado, sumando este término en la ecuación.
Después de encontrar los términos faltantes, ¿cuál es el siguiente paso en la transformación?
-El siguiente paso es igualar la ecuación, sumando los términos que se agregaron al lado derecho de la ecuación.
¿Cómo se factoriza un trinomio cuadrado perfecto?
-Para factorizar, se toma la raíz cuadrada del primer y último término y se expresan como un binomio elevado al cuadrado.
¿Qué información se obtiene al final del proceso de transformación?
-Al final, se obtiene el centro de la circunferencia, que es (2, 2), y el radio, que es 4, ya que es la raíz cuadrada de 16.
¿Cuáles son los cuatro pasos mencionados para transformar una ecuación general en una ecuación ordinaria?
-1. Agrupar términos y variables. 2. Buscar trinomios cuadrados perfectos. 3. Igualar ecuaciones. 4. Factorizar.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
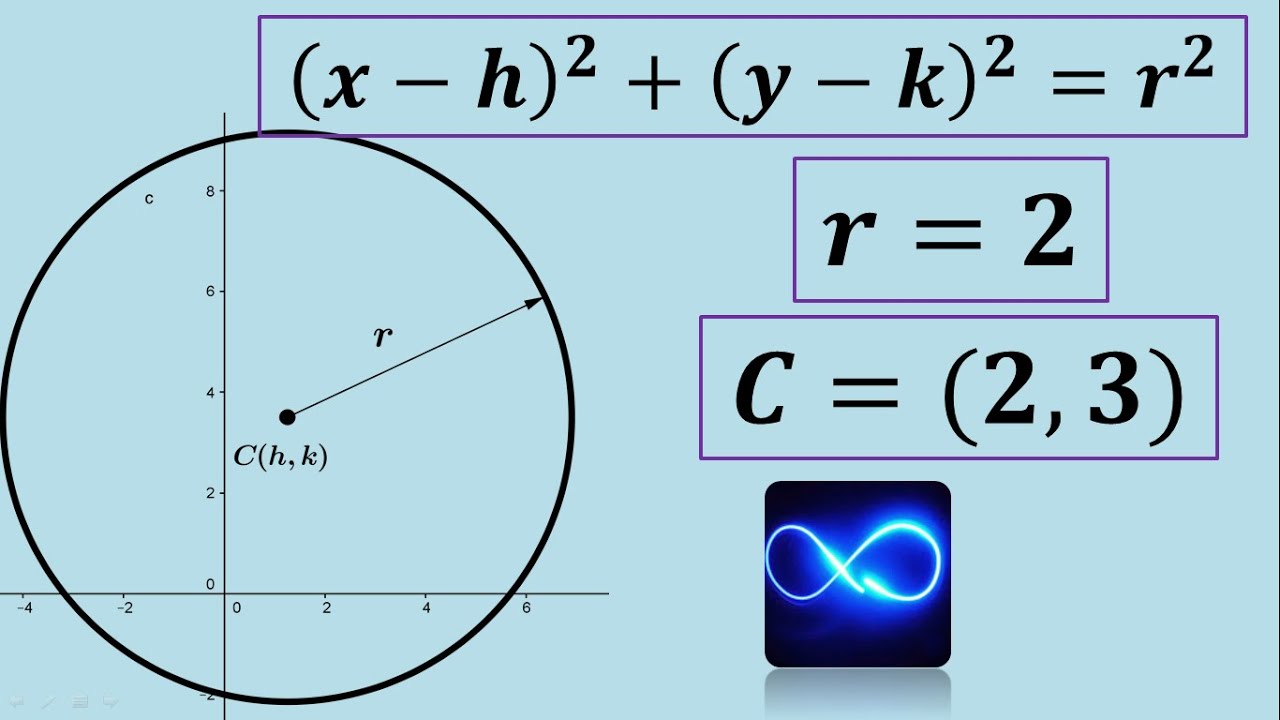
Ordinary and general equation of circumference with given center and radius (Example 1)

Ecuación de la circunferencia con centro fuera del origen (cuarta parte)

Find center and radius of circumference (completing perfect square trinomial)

Ecuación de la circunferencia con centro fuera del origen (tercera parte).

circunferencia que pasa por tres puntos

21. Encontrar la pendiente de una recta dada la ecuación general
5.0 / 5 (0 votes)
