Angular Motion | Sport Science Hub: Biomechanics Fundamentals | Updated 2021 No Music
Summary
TLDRThis video from the Sports Science Hub delves into the fundamentals of angular motion, explaining key concepts such as torque, angular displacement, and angular velocity. It highlights the importance of moment of inertia and angular momentum, emphasizing their relationships and the impact of mass distribution. The video also outlines Newton's laws of angular motion, including conservation of angular momentum and the laws of angular acceleration and reaction. Designed to enhance understanding of rotational dynamics, this guide is essential for anyone interested in the principles governing movement in sports science.
Takeaways
- 🎢 Angular motion refers to movement around a fixed point or axis, resulting from external forces applied outside the center of mass.
- 🔄 Torque is the rotational force that causes an object to turn, calculated as the force multiplied by the distance from the fulcrum.
- 📏 Angular distance measures the total angle rotated about an axis, expressed in degrees or radians (e.g., a complete pirouette is 360 degrees).
- ↔️ Angular displacement is the smallest angle change between the starting and finishing points, also measured in degrees or radians (e.g., a pirouette can have 0 degrees of angular displacement).
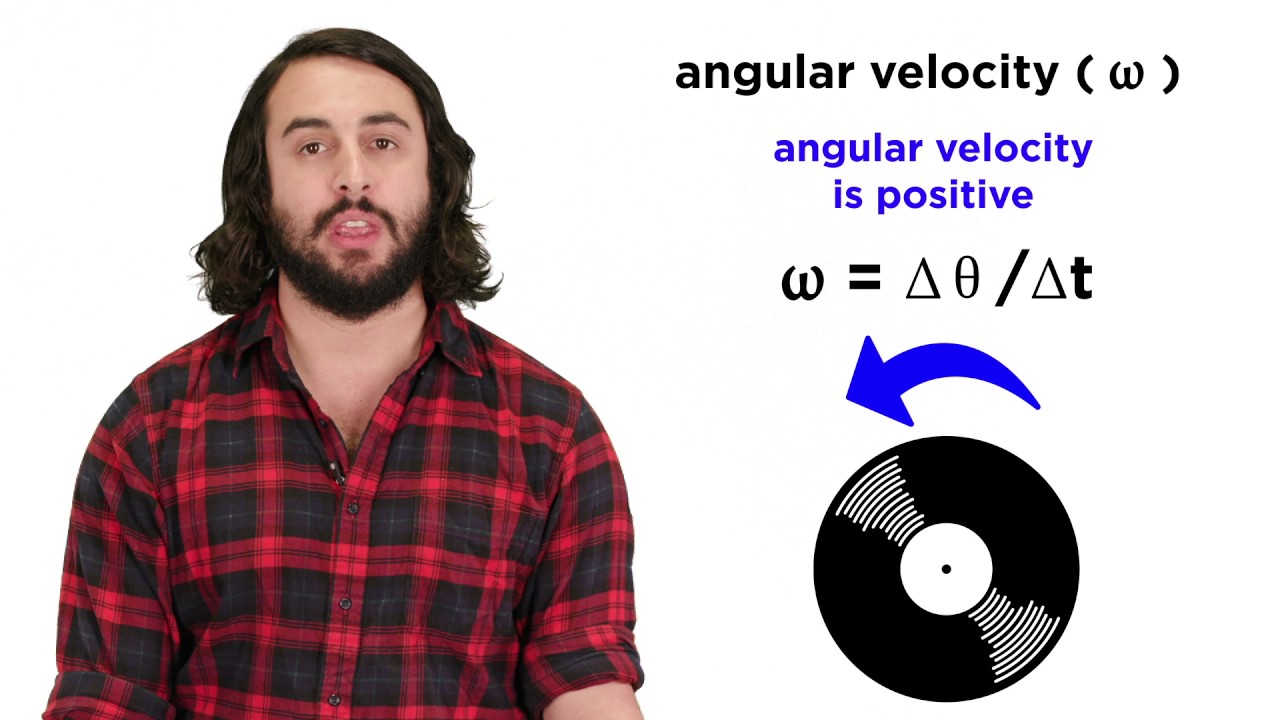
- ⏱️ Angular velocity indicates the rate of change of angular displacement, measured in radians per second, calculated by dividing angular displacement by time.
- 📈 Angular acceleration refers to the rate of change of angular velocity, expressed in radians per second squared, calculated as angular velocity divided by time.
- ⚖️ Moment of inertia represents an object's resistance to angular motion, influenced by mass and its distribution around the axis; a tucked somersault has a lower moment of inertia than a straight one.
- 🌪️ Angular momentum is the product of an object's moment of inertia and its angular velocity, demonstrating an inverse relationship between them.
- ⚖️ Newton's laws of angular motion are analogous to his laws of motion and include the conservation of angular momentum and relationships involving torque.
- 🔄 The law of conservation of angular momentum states that a rotating body continues with constant angular momentum unless acted upon by an external force.
Q & A
What is angular motion?
-Angular motion is the movement of an object around a fixed point or axis, typically occurring when a force is applied outside the center of mass.
What is torque, and how is it calculated?
-Torque is the rotational force that causes an object to turn around its axis of rotation. It can be calculated by multiplying the force applied by the distance from the fulcrum (moment arm).
What is the difference between angular distance and angular displacement?
-Angular distance is the total angle rotated about an axis, measured in degrees or radians. Angular displacement is the smallest change in angle between the starting and finishing points, which can also be measured in degrees or radians.
How is angular velocity defined and measured?
-Angular velocity is the rate of change of angular displacement or the rate of spin, measured in radians per second. It can be calculated by dividing angular displacement by time.
What does angular acceleration represent?
-Angular acceleration represents the rate of change of angular velocity, measured in radians per second squared. It can be calculated by taking the change in angular velocity over time.
What is moment of inertia, and what factors affect it?
-Moment of inertia is the resistance of a body to angular motion or rotation. It depends on the mass of the body and the distribution of that mass relative to the axis of rotation.
How does an athlete increase their angular velocity?
-An athlete can increase their angular velocity by bringing their mass closer to the axis of rotation, thereby reducing their moment of inertia.
What is angular momentum, and how is it related to inertia and angular velocity?
-Angular momentum is the product of moment of inertia and angular velocity. It is inversely proportional, meaning when one increases, the other decreases.
What are Newton's laws of angular motion?
-Newton's laws of angular motion include: 1) A rotating body will maintain constant angular momentum unless acted upon by an external force, 2) Angular acceleration is proportional to the torque causing it, and 3) For every torque exerted by one body on another, there is an equal and opposite torque exerted back.
Why is the law of conservation of angular momentum important?
-The law of conservation of angular momentum is important because it explains how a rotating body continues to spin at a constant rate unless influenced by external forces, which is crucial in various sports and physical activities.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)