03. Vectores y puntos en tres dimensiones (Coordenadas tridimensionales)
Summary
TLDREn este video de 'Mate, fácil', se introduce el sistema de coordenadas rectangulares tridimensionales, que es esencial para comprender otros sistemas como las coordenadas esféricas y cilíndricas. Se explica cómo agregar un tercer eje perpendicular a los ejes x e y, formando un sistema tridimensional. Se utiliza el software GeoGebra para visualizar mejor los puntos y vectores en el espacio 3D. Además, se detallan operaciones básicas como la suma de vectores y el producto por un escalar, preparando el terreno para interpretaciones geométricas en futuros videos del curso.
Takeaways
- 📐 El video explica el sistema de coordenadas rectangulares tridimensionales, esenciales para entender otros sistemas como el esférico y el cilíndrico.
- 🔀 Al agregar una tercera recta perpendicular a las otras dos, se obtiene un sistema tridimensional con los ejes X, Y y Z.
- 🖼️ La representación gráfica de la tercera dimensión en una hoja utiliza la perspectiva, similar a cómo se dibuja un cubo.
- 🔺 Los ejes se nombran como X (horizontal), Y (profundidad) y Z (vertical), lo que facilita la representación de funciones de dos variables.
- ✏️ Los planos coordenados (XY, XZ, YZ) se utilizan para ubicar puntos y dibujar figuras en el espacio tridimensional.
- 📊 Para graficar un punto en tres dimensiones, se necesitan tres coordenadas: X, Y y Z, que indican la posición en cada eje.
- 🔗 Un prisma ayuda a visualizar las coordenadas de un punto en el espacio, utilizando rectas perpendiculares y paralelas a los ejes.
- ➡️ Los vectores en el espacio tridimensional se representan con tres componentes (X, Y, Z) y se pueden mover libremente en el espacio.
- ➕ Las operaciones con vectores incluyen la suma, que se realiza componente por componente, y el producto por un escalar, multiplicando cada componente por un número real.
- 🎯 El video promete mostrar más adelante cómo interpretar geométricamente las operaciones con vectores en tres dimensiones.
Q & A
¿Por qué se llama sistema de coordenadas rectangulares tridimensional?
-Se llama sistema de coordenadas rectangulares porque, a diferencia de otros sistemas de coordenadas como las esféricas y cilíndricas, utiliza ejes perpendiculares entre sí. Es tridimensional porque considera tres ejes (x, y, z) para representar puntos en el espacio.
¿Qué representan los ejes x, y y z en un sistema tridimensional?
-En un sistema tridimensional, el eje x suele representar la dirección horizontal hacia la derecha, el eje y la dirección horizontal hacia adelante o hacia atrás, y el eje z la dirección vertical hacia arriba y abajo.
¿Cómo se representa un punto en el espacio tridimensional?
-Un punto en el espacio tridimensional se representa mediante tres coordenadas (x, y, z), donde x indica la posición en el eje x, y en el eje y, y z en el eje z.
¿Por qué se utiliza la perspectiva para representar el eje z en un plano?
-Se utiliza la perspectiva para representar el eje z porque, al dibujar en una superficie plana, no podemos mostrar directamente la tercera dimensión. La perspectiva ayuda a simular la profundidad, haciendo que el eje z parezca inclinado aunque realmente sea perpendicular a los otros ejes.
¿Qué es el origen en un sistema de coordenadas tridimensional?
-El origen es el punto donde se intersectan los tres ejes (x, y, z). En el origen, las coordenadas son (0, 0, 0). Es el punto de referencia a partir del cual se mide la posición de otros puntos en el espacio.
¿Qué son los planos coordenados y cómo se definen?
-Los planos coordenados son los planos formados por dos ejes. En el sistema tridimensional, tenemos tres: el plano xy (formado por los ejes x e y), el plano xz (formado por los ejes x y z), y el plano yz (formado por los ejes y y z).
¿Cómo se suma un vector en tres dimensiones?
-Para sumar dos vectores en tres dimensiones, sumamos cada una de sus componentes. Si tenemos el vector u = (3, 1, -2) y el vector v = (2, -4, 1), la suma sería u + v = (3+2, 1-4, -2+1) = (5, -3, -1).
¿Qué significa multiplicar un vector por un escalar?
-Multiplicar un vector por un escalar significa multiplicar cada una de las componentes del vector por ese número. Por ejemplo, si el vector es u = (2, 3, -5) y el escalar es 4, el producto sería 4 * u = (2*4, 3*4, -5*4) = (8, 12, -20).
¿Cómo se representa geométricamente un vector en el espacio tridimensional?
-Un vector en el espacio tridimensional se representa como una flecha que tiene una dirección, sentido y magnitud. Puede comenzar en cualquier punto, pero suele representarse desde el origen hasta un punto final (x, y, z) para facilitar su estudio.
¿Por qué es útil el uso de software como GeoGebra para entender el sistema de coordenadas tridimensional?
-El software como GeoGebra facilita la visualización de los ejes, puntos y vectores en el espacio tridimensional. Esto permite rotar y ver diferentes perspectivas del sistema, lo que ayuda a comprender mejor las relaciones espaciales y la disposición de los elementos en 3D.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Cálculo integral triple con cilindro y esfera | Coordenadas Cilíndricas y Esféricas | [LARSON 14.7]

78. GEOMETRÍA ANALÍTICA: COORDENADAS POLARES

2-1 a 2-3 Introducción, Posición y Orientación de un Cuerpo Rígido (Curso: Fundamentos de Robótica)

Cálculo del volumen I Ejemplo 2
Convertir coordenadas polares a rectangulares (cartesianas)
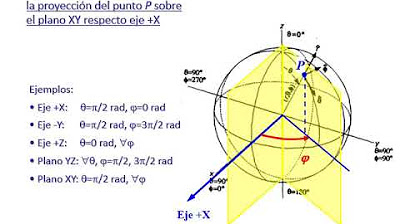
Coordenadas esféricas para el estudio de antenas | | UPV
5.0 / 5 (0 votes)
