Altair Compose: Signal Processing - Power Spectral Density

Summary

This lecture introduces power spectral density (PSD) and its computation using the Discrete Fourier Transform (DFT) and the Welch method, which offers a robust way to estimate PSD in noisy signals. The lecture explains how PSD represents the distribution of signal power across frequencies and provides formulas to calculate both single-sided and double-sided PSDs. It also covers signal processing challenges like noise and frequency resolution, and demonstrates how the Welch method mitigates these issues through segmentation and overlapping. Finally, it shows practical PSD calculation using Compose, emphasizing key advantages and trade-offs.

Takeaways

• 📊 The lecture introduces Power Spectral Density (PSD), a method to represent the power of a signal distributed over a frequency spectrum.
• 📐 PSD is calculated by dividing the spectral power by the frequency range, often using the Discrete Fourier Transform (DFT) or Fast Fourier Transform (FFT).
• 🎛️ The difference between double-sided and single-sided PSDs is explained, with single-sided PSD requiring a folding process of the double-sided PSD.
• 💡 The Welsh method is introduced as a more robust algorithm for estimating PSD, useful for handling noisy or non-deterministic signals.
• 📈 The Welsh method divides a signal into overlapping segments, applies a window function, computes FFTs, and averages the PSDs to provide a more accurate representation.
• 🔄 Overlapping segments in the Welsh method ensure no loss of critical information that might occur at the edges of windows in the signal.
• 🧮 The lecture emphasizes that PSD is a density measurement, meaning it is normalized by frequency resolution, which is crucial for interpreting the results.
• ⚖️ It highlights the trade-off in using the Welsh method: while it reduces noise, it also lowers frequency resolution.
• 🔧 The practical implementation of PSD computation is shown using the Compose tool, leveraging built-in functions such as 'P Welch' to simplify the process.
• 🎮 The provided app allows users to experiment with different parameters (e.g., window type, overlap, window length) to visualize their effects on the PSD and signal.

Q & A

What is Power Spectral Density (PSD)?

Power Spectral Density (PSD) represents the power of a signal distributed over its spectrum of frequencies. It describes how the power of a signal varies with frequency and is defined as power per unit frequency.

How is the Power Spectral Density (PSD) computed using the Discrete Fourier Transform (DFT)?

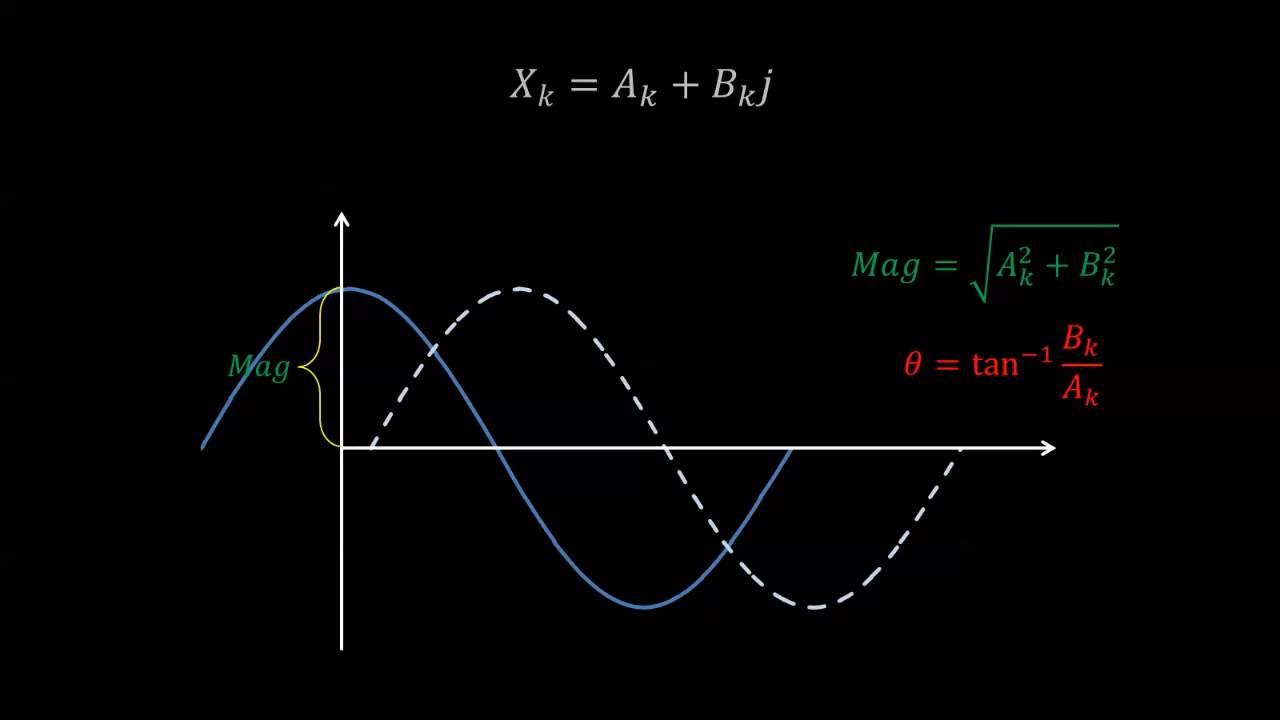
The PSD is computed by squaring the Discrete Fourier Transform (DFT) coefficients and then dividing by the number of coefficients to get the spectral power. The spectral power is then divided by the frequency range, which for a double-sided DFT, is the sampling frequency.

What is the difference between single-sided and double-sided PSD?

Double-sided PSD considers both positive and negative frequencies, while single-sided PSD focuses only on positive frequencies. The single-sided PSD is computed by folding the double-sided PSD and doubling the values, except for the mean and Nyquist frequency components.

What is the Parseval’s Theorem and how is it related to PSD?

Parseval’s Theorem states that the total energy of a signal can be computed equivalently in time or frequency domains. In the context of PSD, it implies that the sum of power in the time domain can be represented as the sum of spectral power in the frequency domain.

What are the advantages of the Welch method for PSD estimation?

The Welch method improves PSD estimation by averaging over multiple segments of a signal, which reduces noise and provides a better representation of the signal’s power spectrum. It also helps in estimating the PSD for non-deterministic processes.

Why is it important to use windowing in the Welch method?

Windowing helps reduce spectral leakage by minimizing the discontinuities at the edges of each segment. This allows for a more accurate estimation of the PSD, especially when dealing with overlapping segments in the Welch method.

How does the overlap of segments affect the Welch method?

Overlapping segments in the Welch method increases the usage of signal data, especially at the edges where the window function reduces the signal's impact. This leads to a more efficient use of the signal and provides a better estimate of the PSD.

What are the effects of noise on PSD computation?

Noise affects the accuracy of PSD computation by introducing additional power across the frequency spectrum. Averaging multiple segments in the Welch method helps reduce the impact of noise and provides a more robust estimate of the true PSD.

How does the length of the FFT affect the PSD resolution?

The length of the FFT determines the frequency resolution of the PSD. A longer FFT provides finer frequency resolution but may require zero-padding if the signal length is shorter. A shorter FFT reduces resolution but may be faster to compute.

What are some common applications of PSD analysis?

PSD analysis is used in signal processing to identify the frequency components of a signal, detect noise levels, and analyze random processes. It is commonly applied in fields such as telecommunications, audio processing, and vibration analysis.