8of24 anlizing and FFT Basic signal processing theory with IIR filter design with pole zero placemen

Summary

The video explains the process of signal sampling and frequency analysis using Fourier Transform. It covers how to sample signals at specific intervals, process the data using Discrete Fourier Transform (FFT), and analyze frequency components in noisy signals. The speaker demonstrates the calculation of frequency peaks, showing how to identify the amplitude of specific signals within a complex waveform. This process is crucial for testing circuits, filtering noise, and optimizing signal clarity, allowing engineers to understand and manipulate the frequencies present in a given signal.

Takeaways

• 😀 The sampling rate must be at least twice the highest frequency in the signal (Nyquist theorem) to ensure accurate signal representation.
• 😀 A signal can be simulated to test circuits before using real-world signals from analog inputs.
• 😀 Fourier Transform (FT) is used to convert a signal from the time domain to the frequency domain, where it can be analyzed in terms of its frequency components.
• 😀 The Discrete Fourier Transform (DFT) is used for analyzing discrete signals, and the Fast Fourier Transform (FFT) is a faster algorithm for the same process.
• 😀 Signal analysis with Fourier Transform involves summing sine and cosine waves to reconstruct the original signal.
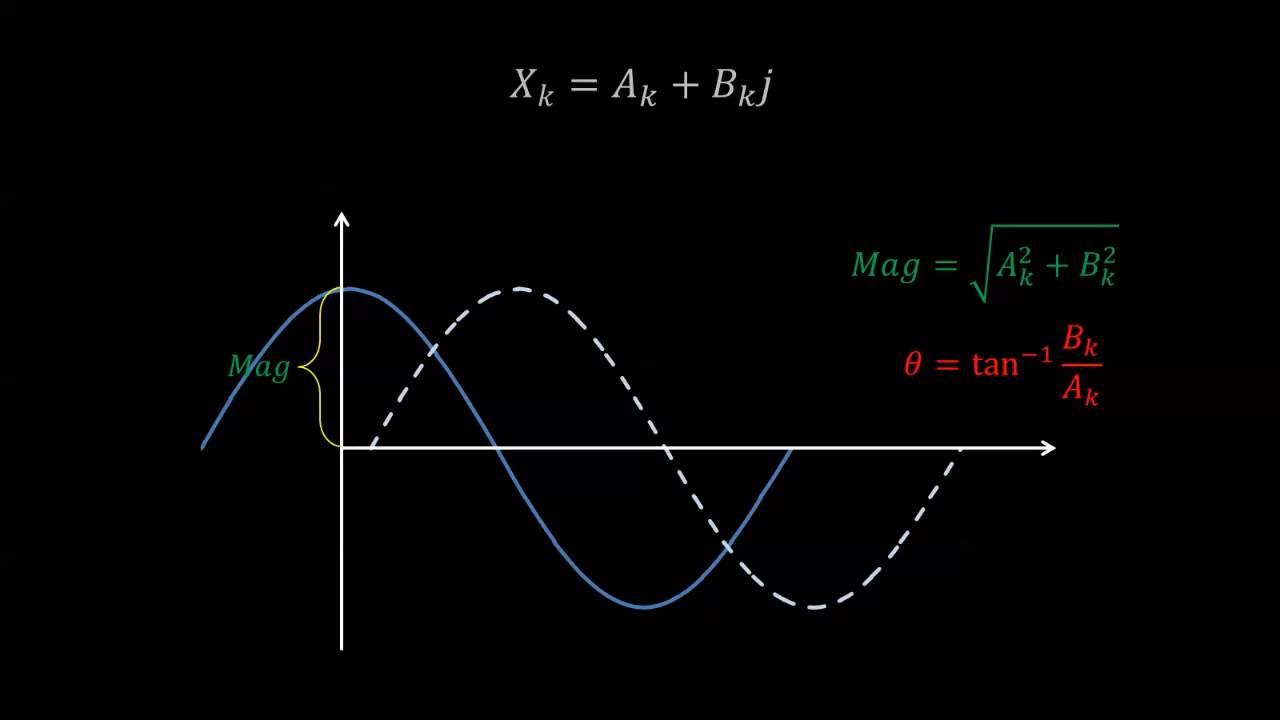
• 😀 The real and imaginary parts of Fourier coefficients represent the amplitude and phase shifts of the signal's frequency components.
• 😀 If a signal matches a specific frequency, its corresponding Fourier Transform value will be large; otherwise, it will be small.
• 😀 By performing Fourier analysis on a signal, it’s possible to identify noise and unwanted frequency components.
• 😀 The Fourier Transform can be used to decompose complex signals into simpler sine and cosine components, which can then be analyzed individually.
• 😀 Practical applications of Fourier analysis help in filtering out noise from signals and understanding the frequency components present in real-world circuits.

Q & A

What is the relationship between sampling frequency and signal frequency in the script?

The script explains that the sampling frequency must be at least double the highest frequency of the signal to avoid aliasing. This is based on the Nyquist theorem, ensuring accurate signal reconstruction.

How does the script simulate the signal before applying the Fourier Transform?

The script uses a simulated signal with a 200 Hz sampling rate. This simulation allows the user to observe the behavior of the signal and its components before real-world input is used in the system.

What is the main purpose of using the Fourier Transform in the context of this script?

The main purpose of the Fourier Transform is to analyze and decompose complex signals into their constituent frequencies. It helps identify the frequency components of the signal, enabling better understanding and manipulation of the data.

How does the Fourier Transform formula work in this context?

The Fourier Transform formula uses complex exponentials (e^jθ), which break down the signal into sine and cosine components. These components are then correlated with the signal to identify the frequencies present.

Why is it important to use the absolute values when performing the Fourier Transform?

The absolute values are used in the Fourier Transform to account for phase shifts. By using absolute values, the calculation remains valid even if the signal is out of phase with the reference sine and cosine components.

What does the script mean when it says that the Fourier Transform will show 'spikes' at specific frequencies?

The 'spikes' refer to peaks in the frequency domain representation of the signal. These spikes indicate the presence of specific frequencies within the signal, such as a 2 Hz or 50 Hz sine wave, as described in the example.

How is the concept of adding sine waves used in the script?

The script explains that by adding two sine waves of different frequencies (e.g., 2 Hz and 50 Hz), a noisy signal is formed. This noisy signal can then be analyzed using the Fourier Transform to identify its frequency components.

What role does the frequency analysis play in circuit testing, according to the script?

Frequency analysis, facilitated by the Fourier Transform, helps in testing circuits by allowing engineers to observe the frequency components of the signal and assess how the circuit is processing those components. It is especially useful for detecting noise and validating circuit behavior.

What are the key differences between real and imaginary components in the Fourier Transform, as discussed in the script?

In the Fourier Transform, the real and imaginary components correspond to cosine and sine waves, respectively. The real part represents the in-phase signal, while the imaginary part accounts for any phase shift, which may be adjusted using absolute values for accurate frequency representation.

How does the script suggest validating the results of the Fourier Transform?

The script suggests that by analyzing the correlation between the signal and the generated sine waves (both in-phase and out-of-phase), one can evaluate how well the signal matches the expected frequency components. The result of this analysis helps identify the frequencies and their amplitudes within the signal.