FUNCIÓN CRECIENTE, DECRECIENTE y CONSTANTE

Summary

Este video explica los conceptos de funciones crecientes, decrecientes y constantes. Una función creciente aumenta su valor cuando se incrementa la variable independiente, mientras que una decreciente lo disminuye. Las funciones constantes mantienen un valor fijo sin importar la variación de la variable. Se proporcionan ejemplos gráficos y algebraicos para cada tipo de función, destacando también casos especiales como las funciones compuestas que pueden cambiar su comportamiento según el intervalo. Finalmente, se invita a los espectadores a explorar más contenidos de precálculo en el canal.

Takeaways

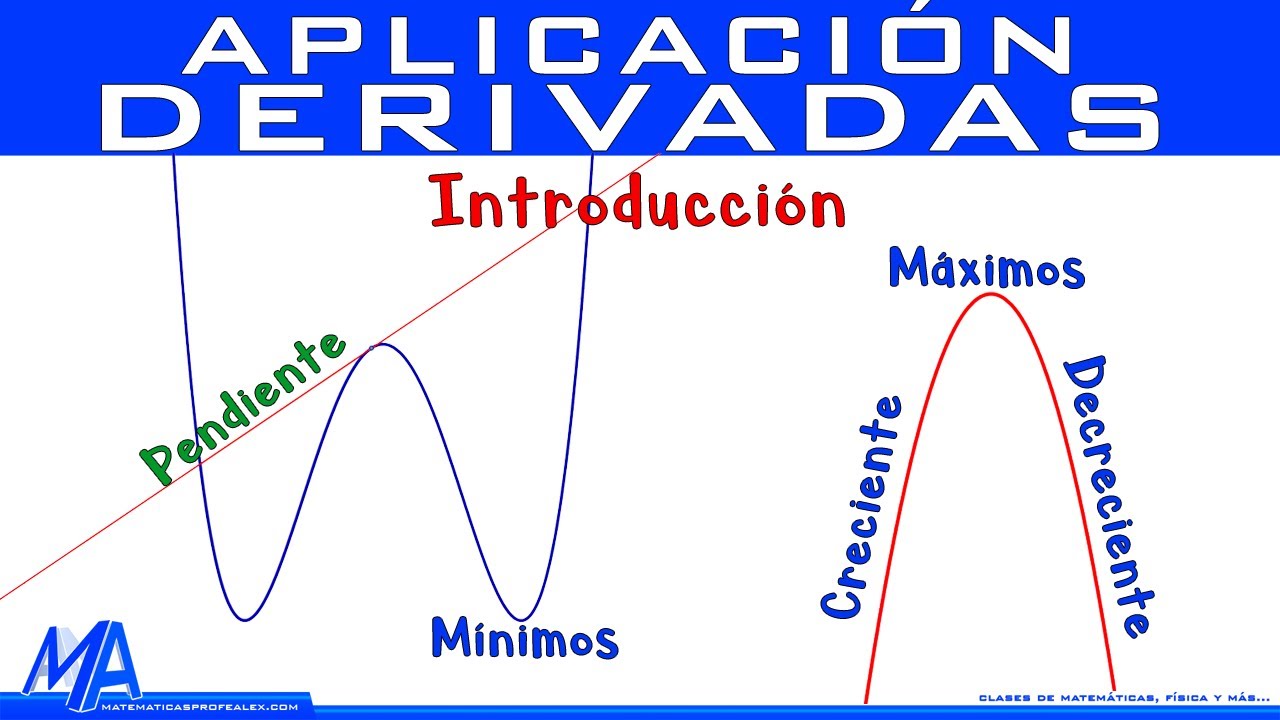
• 📈 Una función creciente es aquella en la que al aumentar la variable independiente (x), aumenta también el valor de la función.
• 🔢 Formalmente, si x2 > x1, entonces f(x2) > f(x1) en una función creciente.
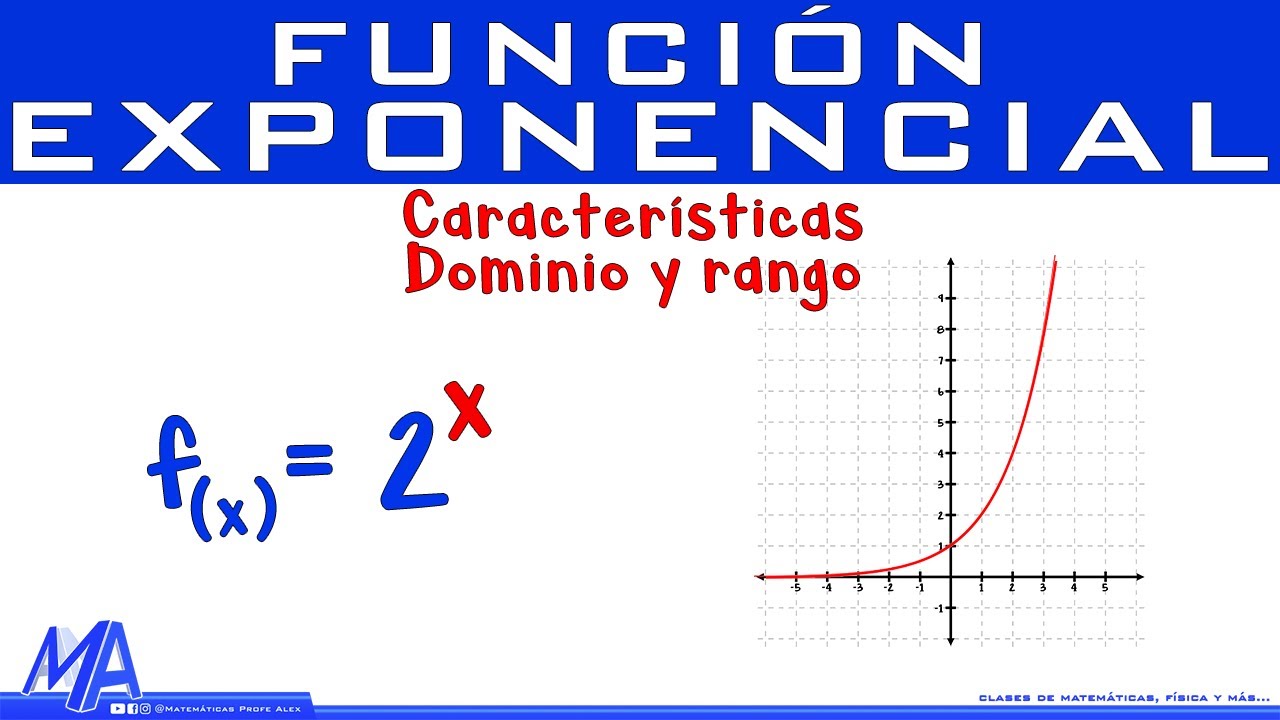
• 🧮 Ejemplos de funciones crecientes incluyen funciones lineales como f(x) = x + 3 y exponenciales como f(x) = 2^x.
• 📉 Una función decreciente es lo opuesto: al aumentar la variable independiente, el valor de la función disminuye.
• 🔄 En funciones decrecientes, si x2 > x1, entonces f(x2) < f(x1).
• 📐 Ejemplos de funciones decrecientes incluyen rectas con pendiente negativa y exponentes negativos en funciones exponenciales.
• ➖ Las funciones constantes son aquellas donde el valor de la función no cambia, sin importar el valor de x.
• 📏 Ejemplos de funciones constantes incluyen f(x) = -7/2 y f(x) = 0, que son rectas paralelas al eje x.
• 🔀 Algunas funciones pueden ser crecientes, decrecientes o constantes en diferentes intervalos, como las parábolas o funciones a trozos.
• 🎬 Se pueden encontrar más vídeos educativos sobre funciones en el canal del autor.

Q & A

¿Qué es una función creciente?

Una función creciente es aquella en la que al aumentar el valor de la variable independiente (generalmente x), también aumenta el valor de la variable dependiente (generalmente y).

¿Cómo se representa de manera formal que una función es creciente?

De manera formal, si x2 es mayor que x1, entonces el valor de la función evaluada en x2 será mayor que el valor de la función evaluada en x1, es decir, f(x2) > f(x1).

¿Qué ejemplos se dan de funciones crecientes?

Algunos ejemplos de funciones crecientes son f(x) = x + 3 y la función exponencial f(x) = 2^x.

¿Qué es una función decreciente?

Una función decreciente es aquella en la que al aumentar el valor de la variable independiente x, disminuye el valor de la variable dependiente y.

¿Cómo se representa de manera formal una función decreciente?

Si x2 es mayor que x1, entonces el valor de la función evaluada en x2 será menor que el valor de la función evaluada en x1, es decir, f(x2) < f(x1).

¿Qué ejemplos se mencionan de funciones decrecientes?

Algunos ejemplos de funciones decrecientes incluyen rectas con pendiente negativa y funciones exponenciales con exponente negativo.

¿Qué es una función constante?

Una función constante es aquella en la que, sin importar el valor de la variable independiente x, el valor de la variable dependiente y permanece igual.

¿Cómo se representa gráficamente una función constante?

Gráficamente, una función constante es una línea recta paralela al eje x.

¿Se pueden combinar los comportamientos crecientes, decrecientes y constantes en una función?

Sí, existen funciones compuestas que pueden ser crecientes, decrecientes y constantes en diferentes intervalos. Un ejemplo es una parábola con concavidad positiva que es decreciente hasta cierto punto y luego creciente.

¿Qué es una función a trozos?

Una función a trozos es aquella que tiene diferentes comportamientos en distintos intervalos. Por ejemplo, puede ser decreciente en un intervalo, constante en otro y creciente en otro.