Block Diagram Algebra and Closed Loop Transfer Functions Intro
Summary
TLDRThis video introduces block diagram algebra, a key tool in process control, especially for analyzing closed-loop transfer functions. It walks through the components of a closed-loop system, such as set points, controllers, processes, and measurement devices, explaining how errors are processed and how outputs respond to changes. The explanation highlights the importance of the characteristic equation in every transfer function, helping to predict system responses to inputs like disturbances or set point changes. The video concludes with tips on simplifying complex systems using nested loops, similar to circuit diagrams.
Takeaways
- 📊 Block diagram algebra is a valuable tool in process control for understanding closed-loop transfer functions (CLTFs).
- 🔄 In a typical CLTF, a set point is compared to the measured output value, with the difference (error) being processed by a controller (GC).
- ⚙️ The controller interprets the error and adjusts the process input (P), which goes through the system's process transfer function (GP).
- 💥 Disturbances (D) may affect the process output (Y), which is measured by a device (GM), creating a feedback loop.
- 🧮 The goal of block diagram algebra is to determine the system's output response (Y) to changes in set point (YSP) or disturbances (D).
- ➗ A key concept is that the output is determined by the transfer functions, with Y over YSP being defined as GC * GP divided by (1 + GC * GP * GM).
- 📝 The equation’s denominator, called the characteristic equation, is crucial and appears in every transfer function.
- 📐 To evaluate how output responds to disturbance (D), we focus on the blocks between the disturbance and output (Y), using the transfer function GD.
- 📉 In complex systems, block diagrams can be simplified similarly to how circuit diagrams are reduced in physics.
- 🔁 The characteristic equation in any closed-loop system depends on the product of all blocks in the loop, allowing for easier analysis of the system's behavior.
Q & A
What is block diagram algebra, and why is it important in process control?
-Block diagram algebra is a method used to represent and manipulate transfer functions in control systems. It's important in process control because it simplifies the analysis of closed-loop systems, making it easier to determine how the system's output responds to various inputs or disturbances.
What is a CLTF (Closed-Loop Transfer Function), and how does it work?
-A CLTF represents the relationship between the output and input of a closed-loop control system. It includes the setpoint, process, controller, disturbances, and feedback, which together form the control loop. The CLTF helps determine how the system responds to changes in the setpoint or disturbances.
What role does the setpoint play in the closed-loop system?
-The setpoint is the desired value for the system's output, such as a target temperature or pressure. The system compares the setpoint to the actual output, calculates the error (difference), and adjusts the input to minimize the error.
How does the controller (GC) respond to the error in the system?
-The controller interprets the error (difference between the setpoint and the measured output) and adjusts the system's input accordingly. Its purpose is to minimize the error and bring the system's output closer to the setpoint.
What is the characteristic equation in block diagram algebra?
-The characteristic equation is the denominator of the transfer function derived from the system's block diagram. It is crucial because it determines the system's stability and response to changes in inputs or disturbances. In many cases, it takes the form 1 + GC * GP * GM, where GC is the controller, GP is the process, and GM is the measurement function.
How do disturbances affect the closed-loop system?
-Disturbances are external factors that can affect the process output. In block diagram algebra, they are represented by an external signal (D) entering the system. To determine how the output responds to a disturbance, we calculate Y/D, which gives us the transfer function from the disturbance to the output.
What happens when a disturbance signal is introduced into the system?
-When a disturbance enters the system, its impact is evaluated by the transfer function GD, which represents the blocks between the disturbance and the output. This helps determine how much the disturbance affects the system output.
How does block diagram algebra help simplify complex control systems?
-Block diagram algebra allows us to simplify complex control systems by breaking them down into smaller transfer functions. This is similar to simplifying circuit diagrams in physics, allowing us to analyze nested loops or multiple control elements more easily.
What is the significance of transfer functions in control systems?
-Transfer functions are mathematical representations of the relationship between inputs and outputs in a system. They provide a way to model how the system will respond to changes in inputs (e.g., setpoints or disturbances) and are essential for analyzing system behavior.
Why is it important to understand the relationship between the output and the setpoint in a control system?
-Understanding the relationship between the output and the setpoint is crucial because it reveals how the system behaves when the setpoint changes. For instance, it helps predict how quickly the output will reach the desired value, and whether the system will overshoot or oscillate around the setpoint.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
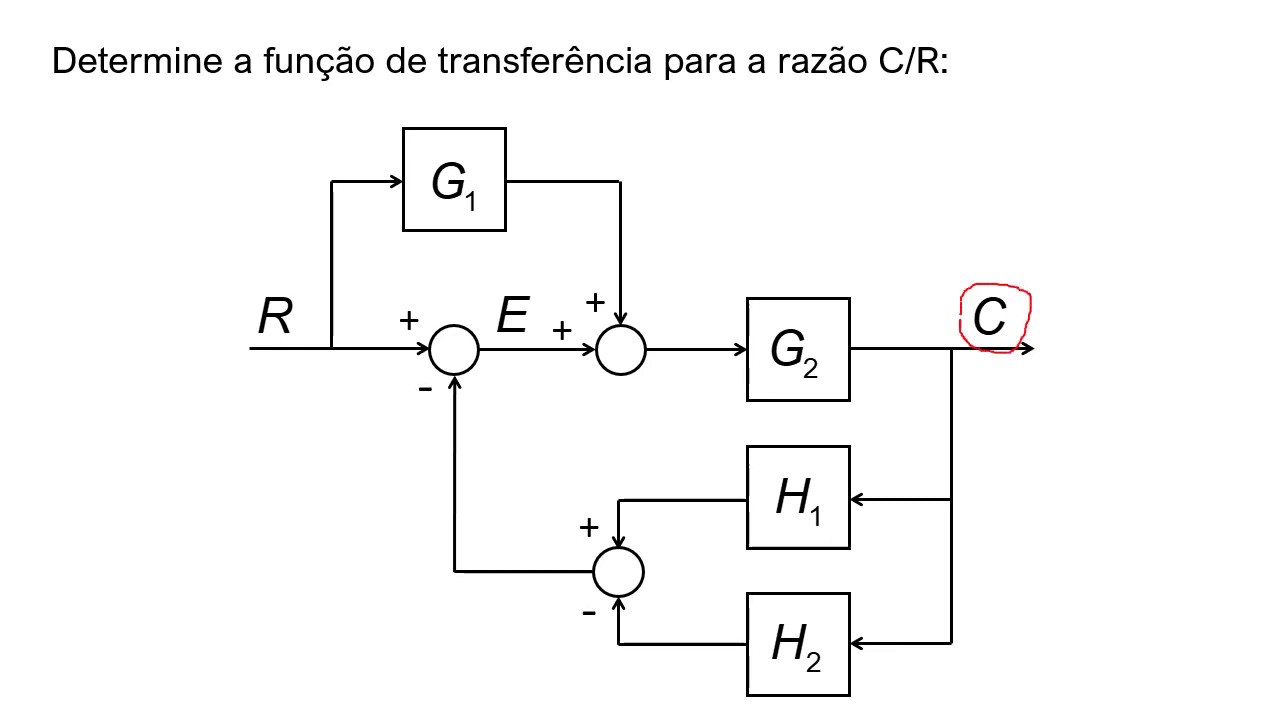
Diagramas de blocos e sua álgebra
What is Control System.Control System Engineering.Open Loop and Closed Loop Control System.Explained

Diagram Blok - 1- Pemodelan dengan diagram blok, komponen utama diagram blok, hubungan antar sistem

Praktikum Dasar Sistem Kendali - Unit 3

Multivariable Closed Loop Control. Identification, Decoupled Control and MIMO Control with Router

06. MG3217 Kendali Proses S02: Penyederhanaan Diagram Blok untuk P, PI
5.0 / 5 (0 votes)