Diagramas de blocos e sua álgebra

Summary

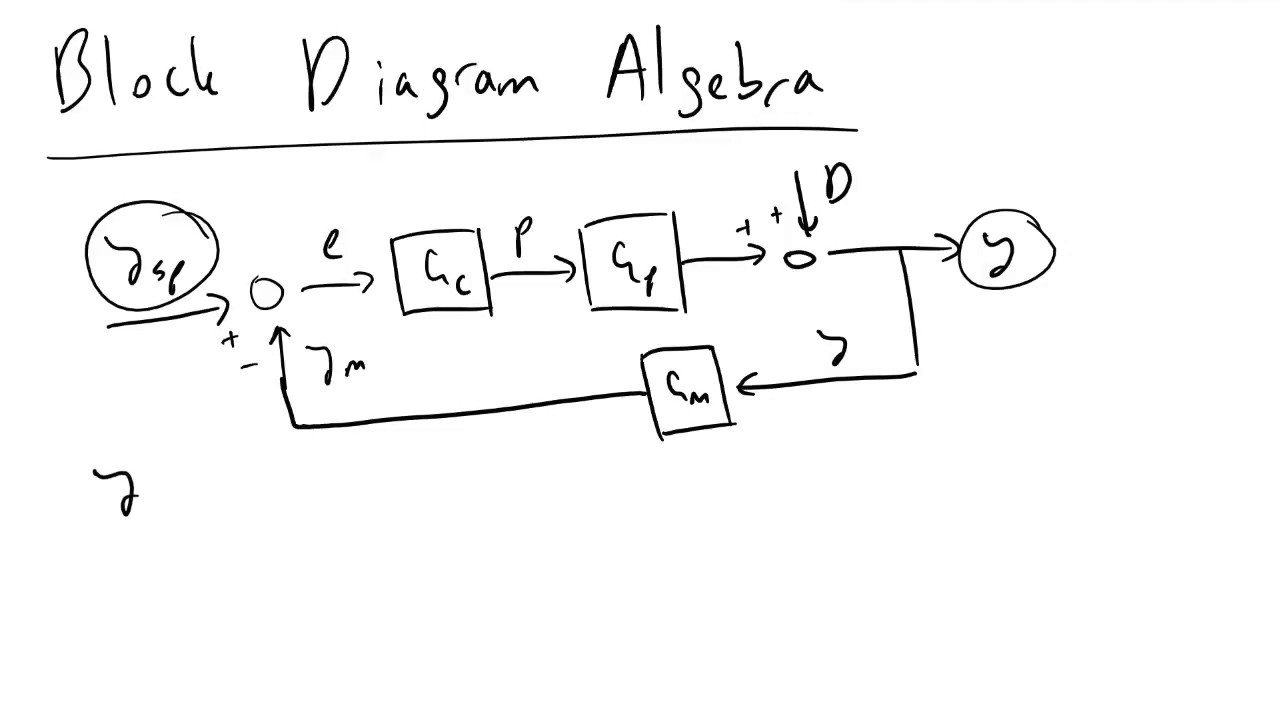
This video focuses on the concepts of block diagrams and block algebra in control systems, explaining how graphical representations of transfer functions help analyze system interactions. The speaker emphasizes the importance of defining intermediate variables to simplify the algebraic deductions required for deriving transfer functions. Through step-by-step algebraic manipulations, the video illustrates how to eliminate intermediate variables and arrive at a final equation based solely on the system's transfer functions, highlighting the process of substitution and simplification. The speaker concludes with insights on reducing complexity and understanding mesh configurations in block algebra problems.

Takeaways

• 😀 Block diagrams are essential for visualizing how transfer functions interact with inputs and outputs in process control systems.
• 😀 Block algebra defines the mathematical operations that can be used to extract equations from graphical representations in block diagrams.
• 😀 A block diagram's complexity can vary depending on the process being analyzed, and complex arrangements are useful for thorough analysis.
• 😀 Understanding the transfer function between the controlled variable and the reference value (set-point) is critical in control problems.
• 😀 The goal in block algebra is to eliminate intermediate variables (like 'a' and 'b') to express equations solely in terms of transfer functions.
• 😀 Defining intermediate variables helps in simplifying the process of writing equations, but it is important to minimize them for clarity.
• 😀 A practical example involves defining two intermediate variables (such as 'a' and 'b') to streamline the algebraic manipulations.
• 😀 Equations that define variables like 'a', 'b', and error are derived from the flow of signals through the blocks and summation points.
• 😀 Substitution and simplification of equations are necessary steps to eliminate unwanted intermediate variables and achieve a desired result.
• 😀 Ultimately, block algebra reduces to algebraic substitution and manipulation, where the goal is to express the output as a function of the transfer functions.
• 😀 The final output, such as a transfer function ratio, should only involve polynomials of the transfer functions and not intermediate variables.

Q & A

What is block algebra, and why is it important?

Block algebra is a set of rules used to manipulate block diagrams, which are graphical representations of transfer functions and their relationships with inputs and outputs. It is crucial because it helps analyze complex systems and derive equations from the graphical representations of these systems.

What role do intermediate variables play in block diagram analysis?

Intermediate variables are used to simplify the process of deriving equations from block diagrams. They help break down the problem into smaller, more manageable parts. The goal is to eliminate these intermediate variables to obtain a final equation that only involves the transfer functions.

Why is it recommended to define intermediate variables using lowercase nomenclature?

Using lowercase nomenclature for intermediate variables helps distinguish them from the main variables and transfer functions, which are typically represented by capital letters in block diagrams. This makes it clear that these are temporary variables used for simplification purposes.

How does block algebra help in reducing the complexity of block diagrams?

Block algebra simplifies block diagrams by eliminating unnecessary intermediate variables and expressing the system's behavior in terms of the transfer functions. This reduction of complexity allows for a clearer understanding of the system and the creation of simpler equations.

What are the steps involved in deriving the transfer function from the block diagram in the given problem?

The steps include defining intermediate variables, writing equations for these variables, and substituting them into each other. The goal is to eliminate intermediate variables and express the desired ratio in terms of the transfer functions. The final result is a transfer function that describes the relationship between the system's input and output.

How are the equations defined for the intermediate variables in this example?

The intermediate variables, 'a' and 'b', are defined based on the signals that pass through specific blocks and summation points in the block diagram. For example, 'a' is defined after a summation point receiving two inputs, and 'b' involves a subtraction of signals coming from blocks h1 and h2.

What is the purpose of eliminating intermediate variables in block diagram analysis?

Eliminating intermediate variables simplifies the system's analysis and helps derive the final transfer function, which expresses the relationship between the system's input and output in terms of the system's transfer functions, making it easier to study and control the system.

What is the significance of the equation 'r/(1 + h1 - h2 * g2)' derived in the example?

This equation represents the final transfer function that describes the interaction between the controlled variable and the set-point. It shows how the system responds to disturbances and how the controlled variable tracks the set-point, given the transfer functions g1, g2, h1, and h2.

How does the substitution process help in deriving the final equation?

Substituting the expressions for intermediate variables into each other allows for the elimination of these variables. By systematically replacing terms and simplifying the equations, the intermediate variables are eliminated, leaving only the transfer functions and the desired ratio in the final equation.

What is the role of experience in improving block diagram analysis?

Experience helps in identifying the most efficient intermediate variables to define, reducing the complexity of the analysis. Over time, an improved understanding of block diagrams and the interactions between different parts of the system allows for more effective simplification and solution of the problems.