Graphing Rational Functions Step-by-Step (Complete Guide 3 Examples)

Summary

This educational video script offers a comprehensive guide to graphing rational functions. It emphasizes the importance of factoring both numerator and denominator, identifying holes and asymptotes, and determining the presence of horizontal or slant asymptotes based on degree analysis. The script walks through three examples, each illustrating different scenarios, including functions with vertical asymptotes, holes, and those approaching horizontal asymptotes. Key points like y-intercepts and x-intercepts are calculated, and the significance of not crossing vertical asymptotes is highlighted. The guide aims to equip viewers with a clear understanding of graphing rational functions step by step.

Takeaways

• 📚 The video provides a comprehensive guide on graphing rational functions, which are ratios of polynomials.
• 🔍 Factoring the numerator and the denominator is the initial step in graphing rational functions, as it helps identify potential holes or removable discontinuities.
• 🕳️ A hole in the graph, or removable discontinuity, occurs when a factor in the numerator cancels out a factor in the denominator.
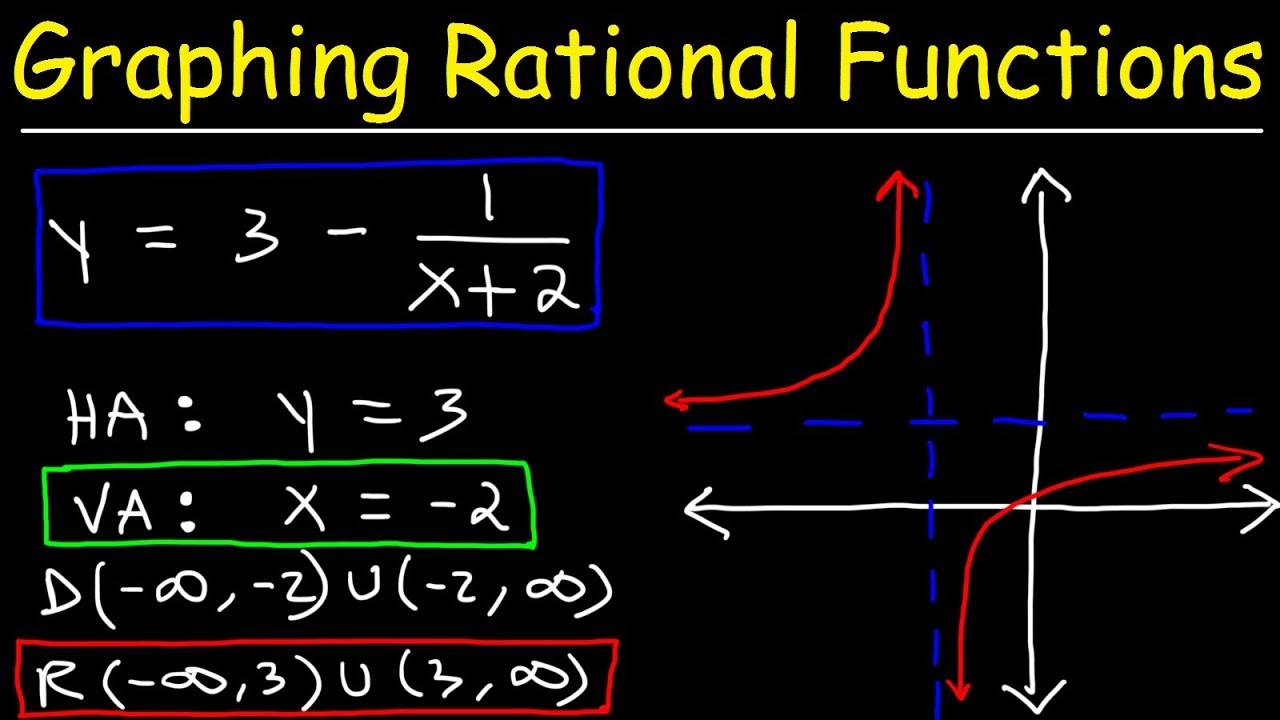
• 🚫 Vertical asymptotes are determined by setting the factors of the denominator equal to zero, as division by zero is undefined.
• 📉 Horizontal or slant asymptotes are analyzed by comparing the highest degree terms in the numerator and the denominator; the relationship between these degrees dictates the type of asymptote.
• 📈 The video demonstrates how to find the y-intercept by setting x to zero and solving, and the x-intercept by setting y to zero and solving.
• 📊 Additional points are plotted by testing values on either side of vertical asymptotes to determine the behavior of the graph as it approaches these lines.
• 🔢 The video uses polynomial long division to determine the equation of a slant asymptote when the degree of the numerator is exactly one higher than the degree of the denominator.
• ✏️ The process of graphing involves sketching the function, marking asymptotes, and plotting key points such as intercepts and additional test points.
• 🔄 The video script emphasizes the importance of understanding the behavior of rational functions near vertical asymptotes, where the function cannot cross or touch these lines due to division by zero.

Q & A

What are rational functions?

Rational functions are mathematical expressions where a polynomial is divided by another polynomial, forming a ratio similar to a fraction.

Why is it important to factor rational functions when graphing them?

Factoring rational functions is crucial for identifying vertical asymptotes, holes, and simplifying the process of graphing by reducing the expression to its simplest form.

What is a hole in the context of graphing rational functions?

A hole is a removable discontinuity in the graph of a rational function, which occurs when a factor in the numerator cancels out a factor in the denominator.

How do you determine if there are any holes in a rational function's graph?

You determine holes by checking if there's a factor in the numerator that cancels with a factor in the denominator after factoring both.

What are vertical asymptotes and how do you find them?

Vertical asymptotes are vertical lines on the graph where the function approaches infinity or negative infinity. They are found by setting the factors of the denominator equal to zero, excluding any factors that would create a hole.

How can you identify if a rational function has a horizontal or slant asymptote?

You identify asymptotes by comparing the degrees of the highest terms in the numerator and the denominator. If the degree of the denominator is higher, there's a horizontal asymptote at y=0. If degrees are equal, the asymptote is the ratio of the leading coefficients. If the numerator's degree is one higher, there's a slant asymptote.

What is the significance of the y-intercept and x-intercept in graphing a rational function?

The y-intercept is the point where the graph crosses the y-axis, found by setting x=0. The x-intercept is where the graph crosses the x-axis, found by setting y=0 and solving for x. These intercepts provide key points for sketching the graph.

Why is it not possible to cross vertical asymptotes on a graph?

You cannot cross vertical asymptotes because it would imply dividing by zero, which is undefined in mathematics.

What is the purpose of plotting additional points when graphing rational functions?

Plotting additional points helps to visualize the behavior of the function near vertical asymptotes and to ensure the graph accurately reflects the function's behavior across the domain.

How does the degree of the polynomial in the numerator compare to the degree of the polynomial in the denominator to determine the type of asymptote?

If the degree of the numerator is less than the degree of the denominator, there is a horizontal asymptote at y=0. If they are equal, the asymptote is the ratio of the leading coefficients. If the numerator's degree is one more than the denominator's, there is a slant asymptote.