Relasi dan Fungsi Matematika Kelas 10 • Part 27: Soal Fungsi Rasional Bentuk 3 - Kuadrat / Linear
Summary
TLDRIn this video, the host explains the concept of rational functions, focusing on the third form of rational function FX = AX² + BX + C / (BX + Q). Key topics include vertical and oblique asymptotes, the x-intercept, y-intercept, and the behavior of the graph. The host demonstrates how to draw the graph, find asymptotes, and calculate critical points. They also discuss the domain and range of the function, emphasizing the limitations caused by vertical asymptotes. The video concludes with a practical example of graphing and analyzing a rational function, providing a clear understanding for viewers.
Takeaways
- 😀 The video discusses rational functions, focusing on a third-degree rational function in the form FX = (AX² + BX + C) / (BX + Q).
- 😀 The video outlines the key elements of the function, including vertical and oblique asymptotes, x and y-intercepts, and extreme points.
- 😀 The vertical asymptote occurs at x = 3, which is represented by a dashed vertical line with arrows pointing upward and downward.
- 😀 The oblique asymptote is given by the equation y = x - 3, and the video shows how to plot this by creating a table of values.
- 😀 The x-intercepts of the function are located at x = 1 and x = 5, while the y-intercept is approximately at y = 1.6.
- 😀 The function graph behavior is explained in different regions: below the oblique asymptote, above the x-axis between 1 and 3, below between 3 and 5, and above again after x = 5.
- 😀 Points such as (-1, -3), (2, 3), (4, 3), and (7, 3) are calculated and plotted to help illustrate the function's graph.
- 😀 The graph approaches both the vertical asymptote at x = 3 and the oblique asymptote as the function continues.
- 😀 The domain of the function is all real numbers except x = 3, which is excluded due to the vertical asymptote.
- 😀 The range of the function is all real numbers, as the graph can move both up and down across the y-axis without bounds.
Q & A
What is the main topic of this video?
-The main topic of the video is the analysis of rational functions, specifically focusing on vertical and oblique asymptotes, x and y-intercepts, and the graphical behavior of the function.
What is the equation of the rational function discussed in the video?
-The equation of the rational function discussed is f(x) = (Ax^2 + Bx + C) / (Bx + Q).
What is the first step in analyzing the graph of the rational function?
-The first step is to analyze the vertical asymptote, which in this case is at x = 3.
What is the significance of the oblique asymptote in the video?
-The oblique asymptote in the video is represented by the line y = x - 3, which is obtained by simplifying the rational function into a linear expression.
How is the graph of the function drawn based on the given function?
-The graph is drawn by first plotting the vertical asymptote at x = 3, then the oblique asymptote, and calculating the points where the function intersects the x and y axes. Additional points are calculated by substituting values of x into the function.
What are the x and y-intercepts of the function?
-The x-intercepts are at x = 1 and x = 5, and the y-intercept is approximately y = 1.6 (or 5/3).
What is the significance of the table used in the video?
-The table is used to calculate specific points on the graph by substituting different x values into the rational function, helping to plot the curve more accurately.
What happens to the graph as x approaches the vertical asymptote?
-As x approaches the vertical asymptote at x = 3, the graph becomes infinitely large or small, depending on the direction (upward or downward).
What is the domain (DF) of the function?
-The domain of the function is all real numbers except x = 3, since x = 3 makes the denominator zero and causes the function to be undefined.
What is the range (RF) of the function?
-The range of the function is all real numbers, as the graph extends both upward and downward without restriction.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
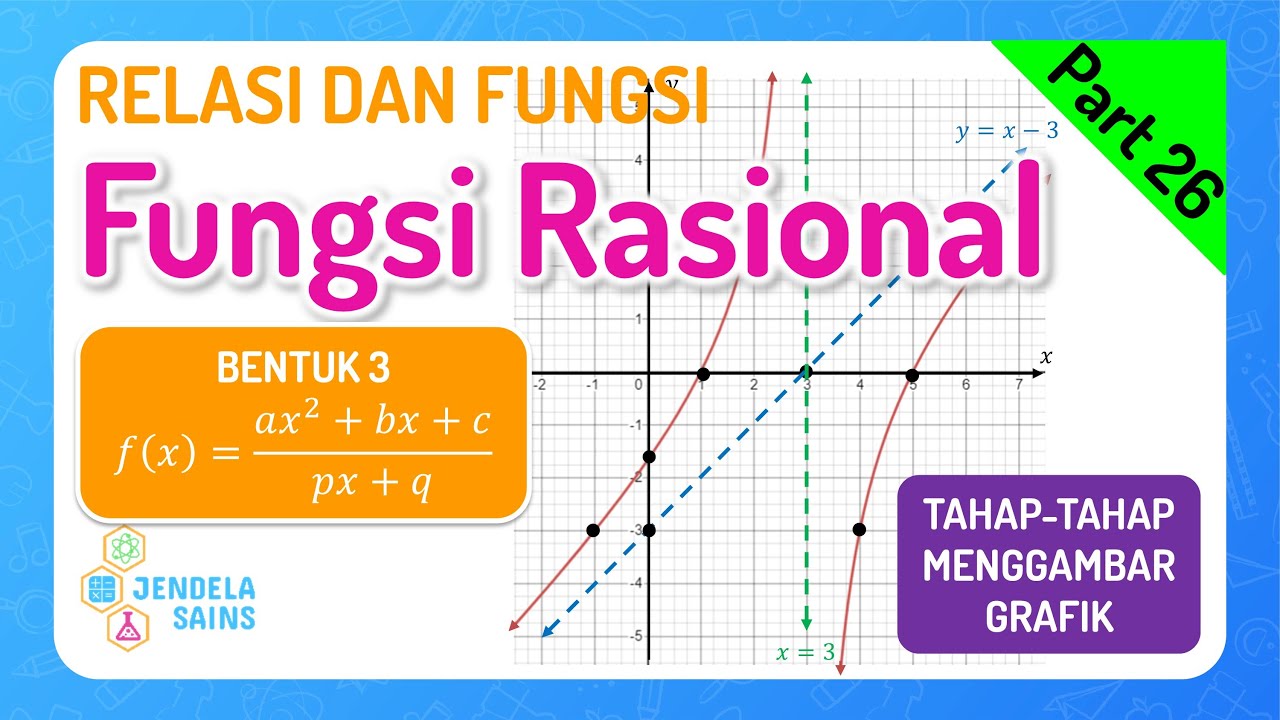
Relasi dan Fungsi Matematika Kelas 10 • Part 26: Fungsi Rasional Bentuk 3 - Kuadrat / Linear
Relasi dan Fungsi Matematika Kelas 10 • Part 24: Fungsi Rasional Bentuk 2 - Linear / Kuadrat
Relasi dan Fungsi Matematika Kelas 10 • Part 22: Fungsi Rasional Bentuk 1 - Linear / Linear

Fungsi Kuadrat (Part 1)

Matematika Kelas 9 : Fungsi Kuadrat (Part 1 : Bentuk umum dan grafik fungsi kuadrat)

TRANSFORMING QUADRATIC FUNCTIONS FROM GENERAL FORM TO STANDARD/VERTEX FORM AND VICE VERSA
5.0 / 5 (0 votes)