Estimar el área bajo una curva usando rectángulos | Comprobando con calculadora
Summary
TLDREn este video, Jesús Granjera enseña cómo estimar el área bajo una curva utilizando rectángulos. El ejemplo práctico utiliza la parábola de x² entre 0 y 1. Jesús explica cómo usar una calculadora para generar una tabla de valores y luego dibujar la curva y los rectángulos correspondientes. Calcula las áreas tanto por encima como por debajo de la curva, y sugiere promediar estos valores para obtener una mejor aproximación. Finalmente, compara su resultado con el valor exacto obtenido usando la integral en la calculadora. Un método práctico para estudiantes de matemáticas.
Takeaways
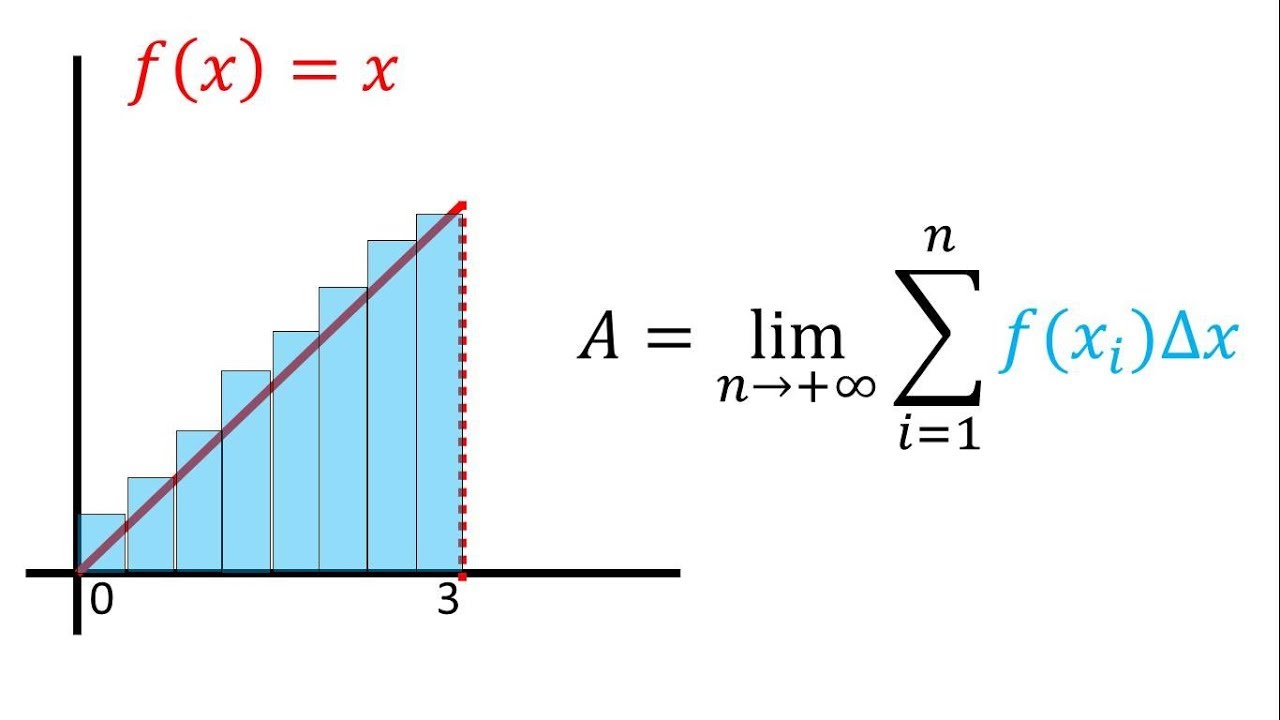
- 📊 El objetivo del video es enseñar cómo estimar el área bajo una curva utilizando rectángulos.
- 📉 El problema a resolver es estimar el área bajo la parábola de x² desde 0 hasta 1.
- 🧮 Utilizan una calculadora para generar una tabla con los valores necesarios para graficar la función.
- 📏 Se traza la gráfica de la parábola y se divide el área en 5 rectángulos, cada uno con una altura diferente.
- 📐 El área de cada rectángulo se calcula multiplicando la base por la altura.
- 🔢 Se suman las áreas de los rectángulos para obtener una aproximación del área total bajo la curva, que da 0.44.
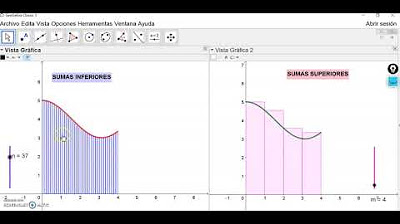
- ⚠️ La aproximación tiene errores, ya que los rectángulos sobrepasan la curva en algunos casos.
- 🔄 Para mejorar la aproximación, se proponen más rectángulos o calcular el área con rectángulos por debajo de la curva.
- 🔗 El área final aproximada se obtiene promediando las áreas de los rectángulos por arriba y por debajo, dando un valor de 0.34.
- 🔢 La integral calculada con la calculadora da un valor de 0.333, lo que indica que la estimación fue bastante cercana.
Q & A
¿Cuál es el objetivo principal del video?
-El objetivo principal del video es enseñar cómo estimar el área bajo una curva usando rectángulos, específicamente bajo la parábola \(x^2\) desde 0 hasta 1.
¿Qué herramienta utiliza el presentador para realizar los cálculos?
-El presentador utiliza una calculadora para realizar los cálculos necesarios y generar una tabla de valores que le permite graficar la curva y estimar el área.
¿Cómo se dividen los intervalos para estimar el área bajo la curva?
-Los intervalos se dividen en segmentos de 0.2, creando cinco rectángulos que cubren el área bajo la curva desde 0 hasta 1.
¿Cómo se calculan las áreas de los rectángulos?
-El área de cada rectángulo se calcula multiplicando la base (0.2) por la altura, que es el valor de la función \(x^2\) en cada punto específico de la tabla generada por la calculadora.
¿Qué estrategia propone el presentador para mejorar la estimación del área bajo la curva?
-El presentador sugiere dos estrategias: aumentar el número de rectángulos para reducir el error y promediar las áreas obtenidas tanto por arriba como por abajo de la curva.
¿Cuál es el valor aproximado del área bajo la curva usando el promedio de áreas por arriba y por abajo?
-El valor aproximado del área bajo la curva es 0.34, obteniendo este valor al promediar el área por arriba (0.44) y el área por abajo (0.24).
¿Cuál es el resultado exacto del área bajo la curva calculado con la integral?
-El resultado exacto del área bajo la curva calculado con la integral es 0.333, que corresponde a \(1/3\).
¿Cómo se podría reducir aún más el margen de error en la estimación del área?
-Para reducir el margen de error, se podrían usar más rectángulos con intervalos más pequeños, lo que daría una estimación más precisa del área bajo la curva.
¿Qué ventaja tiene el método de promediar las áreas por arriba y por abajo de la curva?
-Promediar las áreas por arriba y por abajo de la curva permite obtener una mejor aproximación del área real, ya que equilibra los errores de sobreestimación y subestimación.
¿Qué recomendación hace el presentador al final del video?
-El presentador recomienda suscribirse al canal y compartir el video con compañeros, además de activar la campanita para recibir notificaciones de nuevos videos.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)