VC Dimension
Summary
TLDRThe script discusses computational learning theories, focusing on the concept of hypothesis spaces and their complexity. It explores how certain attributes like X1 and X2 can be defined within a hypothesis space, and how the complexity can be visualized through dimensions. The discussion includes examples of points and lines in a hypothetical space, illustrating the idea of shattering and its implications for learning theories. The script also touches on the limitations of certain formulas and the challenges in applying learning theories to real-world scenarios, concluding with a call for further study in the field of computational learning.
Takeaways
- 📊 The discussion revolves around the concept of hyperparameter space in computational learning theory.
- 🔍 The script explains how the complexity of the model can be adjusted by specifying attributes like X1 and X2.
- 📈 It mentions the use of visualization techniques to understand the high-dimensional complexity, such as using margins to identify points.
- 📝 The concept of labeling points is introduced, where each point can be labeled, and the goal is to find a line that separates these points.
- 🚫 The script notes that not all three points can be separated, leading to the conclusion that the model is shattered.
- 🌐 It provides an example of real-world space where the minimum group of points exists, emphasizing the practical application of the theory.
- 🔢 The script discusses the transition from a hyperplane to a real line, indicating a shift in the model's complexity.
- 🚧 It highlights the limitations when certain constraints are applied, such as not being able to find a convex formula, leading to a shattered model.
- 🔄 The script explores the possibility of dividing points and finding a separator for all possible combinations, emphasizing the complexity of the task.
- 📉 It concludes with the idea that as the number of points increases, the model's complexity and the likelihood of it being shattered also increase.
Q & A
What is the main topic of discussion in the provided transcript?
-The main topic of discussion in the transcript is computational learning theories, specifically focusing on the concept of the hypothesis space and its implications in machine learning.
What does the term 'hypothesis space' refer to in the context of the transcript?
-In the context of the transcript, 'hypothesis space' refers to the set of all possible hypotheses or functions that a learning algorithm can learn.
What is the significance of X1 and X2 being real-valued attributes in the hypothesis space?
-X1 and X2 being real-valued attributes in the hypothesis space indicates that the complexity of the functions or hypotheses that can be learned is high, as real numbers can take any value, thus allowing for a wide range of functions.
What is meant by 'Viz Dimension Complexity' in the transcript?
-The term 'Viz Dimension Complexity' likely refers to the visual representation or visualization of the complexity of the hypothesis space in terms of the number of dimensions.
What does the transcript imply about the relationship between the points P1 and P2?
-The transcript implies that points P1 and P2 can be used to define a line in the hypothesis space, suggesting that they are part of the same linearly separable classification.
Why is the term 'shattering' used in the transcript?
-The term 'shattering' is used to describe the ability of a hypothesis space to perfectly classify all possible points in a dataset without any errors.
What does the transcript suggest about the existence of a real line when points X and Y are considered?
-The transcript suggests that when points X and Y are considered, there is no real line that can separate them positively, indicating that they are not linearly separable.
What does the transcript indicate about the hypothesis space when considering the constraints of a convex function?
-The transcript indicates that when considering the constraints of a convex function, the hypothesis space becomes more restricted, as it cannot find a line that can separate all points, leading to the conclusion that it is not shattering.
What is the implication of the transcript's discussion on the 'PS Learning' and 'PS Learning does not hold' statements?
-The discussion implies that the principles of Probably Approximately Correct (PAC) learning may not always apply, as there are instances where the learning algorithm cannot guarantee to find a hypothesis that is both probably correct and approximately correct.
What does the transcript suggest about the relationship between VC dimension and hypothesis space?
-The transcript suggests that the VC dimension is a measure of the capacity of the hypothesis space, where a higher VC dimension indicates a more complex hypothesis space that can shatter more points.
What conclusion does the transcript draw about the hypothesis space when considering the example with 4 points?
-The transcript concludes that the hypothesis space is not shattering when considering 4 points, as it cannot find a separator for all possible combinations, indicating a limit to the complexity that the hypothesis space can handle.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Krashen's Theory of Second Language Acquisition

8.1 NP-Hard Graph Problem - Clique Decision Problem

2nd Language Theories and Perspectives

117. OCR A Level (H046-H446) SLR18 - 2.1 The need for abstraction
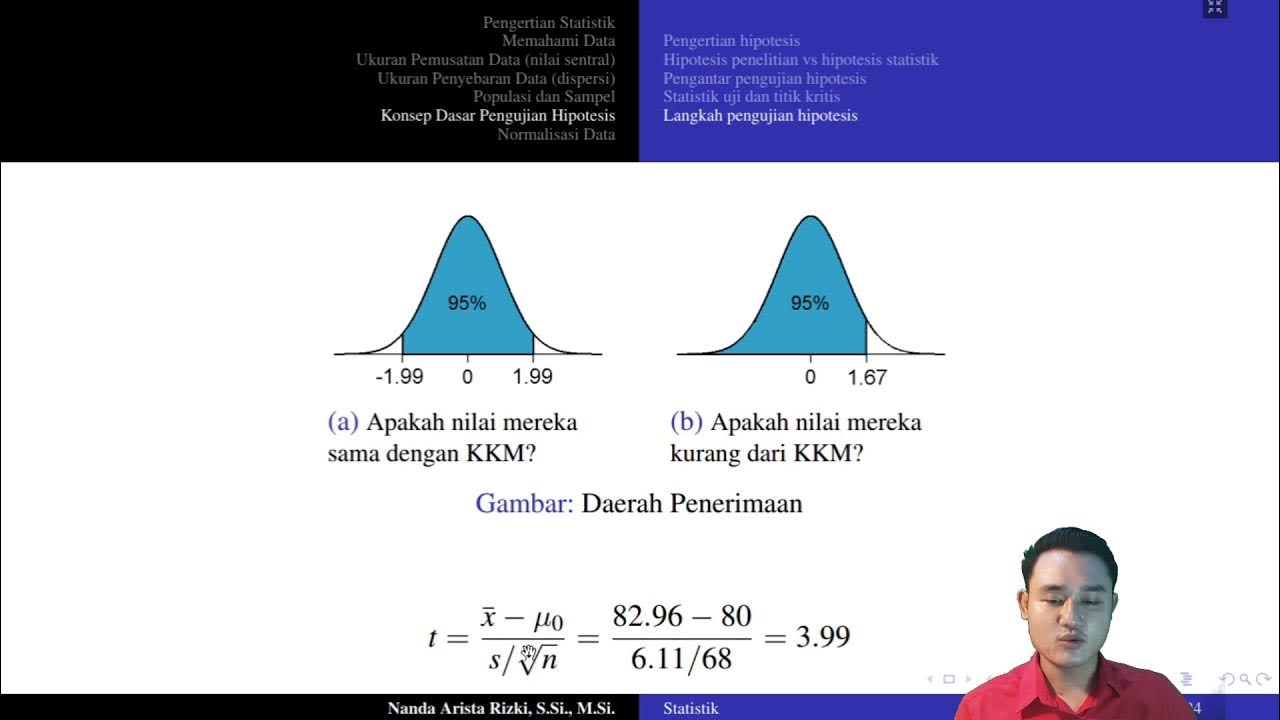
Masih berpikir bahwa hipotesis statistik itu membingungkan? | Statistika

Fact vs. Theory vs. Hypothesis vs. Law… EXPLAINED!
5.0 / 5 (0 votes)