Angle Bisector Construction

geometryvids

27 Feb 201102:16

Summary

TLDRThe video script outlines the process of constructing an angle bisector, a line that divides an angle into two congruent parts. It begins with creating an acute angle and then using a compass to find a point equidistant from the angle's sides. By drawing arcs from the angle's sides and intersecting them, a point on the angle bisector is determined. Finally, a straight edge connects the vertex to this point, resulting in two congruent angles bisected by the angle bisector.

Takeaways

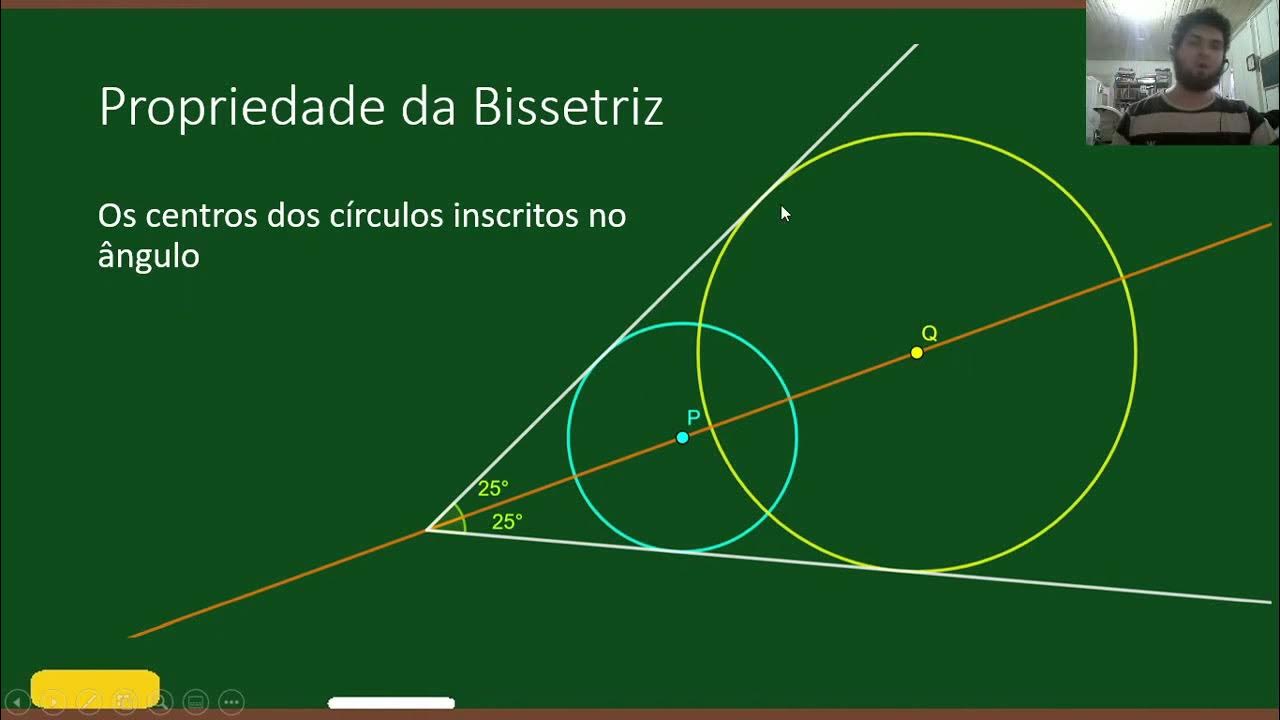
📐 An angle bisector is a line that cuts an angle into two congruent parts.
🖊️ The construction begins by creating an angle, often an acute one, in the middle of the page.
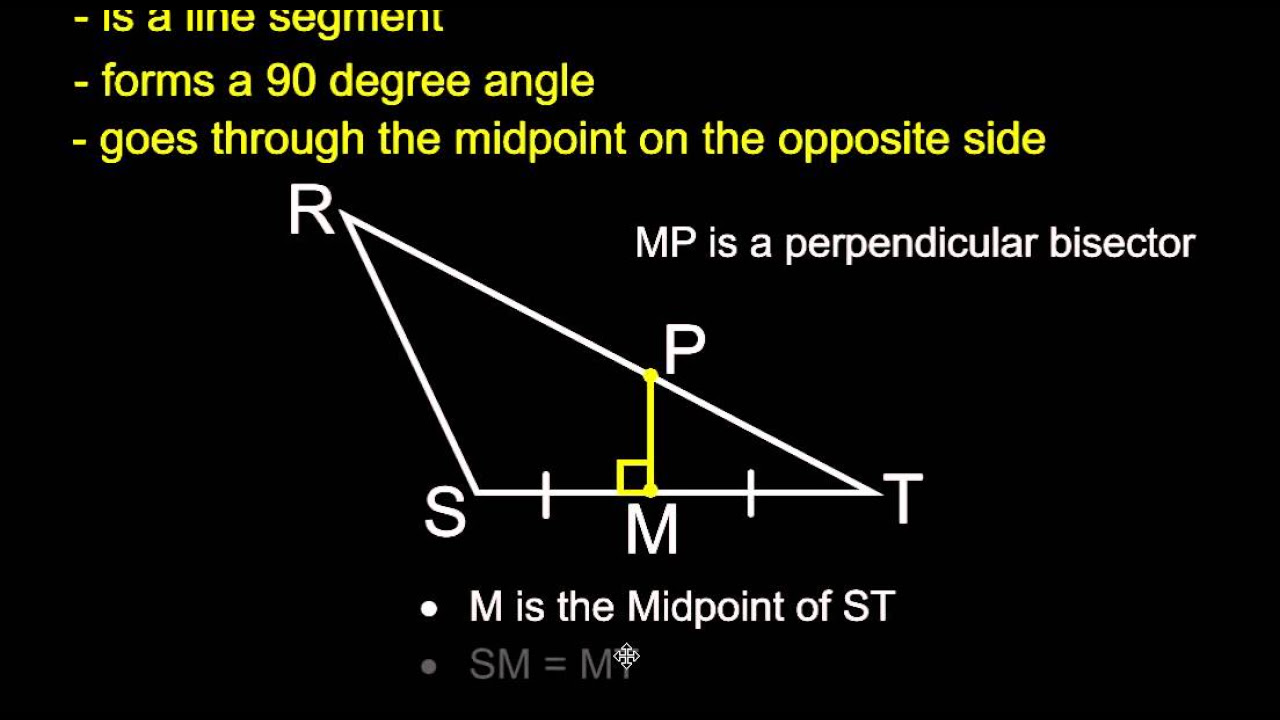
📏 The angle bisector will pass through the vertex of the angle.
⚖️ All points on the angle bisector are equidistant from each side of the angle.
📌 To draw the bisector, we need a second point on the bisector besides the vertex.
🧭 A compass is used to intersect both sides of the angle by drawing an arc.
🔗 Two new intersection points are created where the arc intersects the sides of the angle.
🔄 From each intersection, arcs are drawn again, meeting in the middle of the angle.
🎯 The point where these arcs intersect is equidistant from both sides of the angle.
📏 Using a straight edge, the vertex and this new point are connected to form the bisector, creating two congruent angles.

Q & A

What is an angle bisector?
-An angle bisector is a line that divides an angle into two congruent parts.
Why is it necessary to start with an angle for the angle bisector construction?
-An angle is required to perform the angle bisector construction because the bisector is meant to divide the angle into two equal parts.
What type of angle is constructed in the middle of the page?
-An acute angle is constructed in the middle of the page for the angle bisector construction.
Why does the angle bisector go through the vertex of the angle?
-The angle bisector goes through the vertex because it is the point where the two sides of the angle meet, and the bisector must pass through it to divide the angle into two congruent parts.
What is the significance of the points on the angle bisector being equidistant from the sides of the angle?
-The points on the angle bisector being equidistant from the sides of the angle ensure that the line divides the angle into two congruent angles.
How are the compass settings determined for the angle bisector construction?
-The compass is set to a width that allows it to intersect both sides of the angle, which helps in drawing the arcs necessary for finding the point on the bisector.
What is the purpose of drawing arcs from the intersections created by the compass?
-Drawing arcs from the intersections helps in locating a point that is equidistant from both sides of the angle, which is crucial for determining the angle bisector.
How does the construction ensure that the new point found is equidistant from both sides of the angle?
-The construction ensures the new point is equidistant by having the arcs from both sides intersect at a single point, which by definition is equidistant from both sides.
What tool is used to connect the vertex and the new point found on the bisector?
-A straight edge is used to connect the vertex and the new point to complete the angle bisector construction.
What is the final outcome of the angle bisector construction?
-The final outcome is a line that bisects the original angle into two congruent angles.

Outlines

00:00

📏 Angle Bisector Construction

This paragraph introduces the process of constructing an angle bisector. The angle bisector is a line that divides an angle into two congruent parts. The construction starts with an acute angle drawn in the middle of the page. The bisector is intended to pass through the middle of this angle. A key property of the angle bisector is that all points on it are equidistant from the two sides of the angle. To construct the angle bisector, the process involves using a compass to intersect both sides of the angle and create arcs. These arcs intersect at a point equidistant from both sides of the angle. The construction is completed by drawing a straight line connecting the vertex of the angle and the equidistant point, resulting in two congruent angles bisected by the line.

Mindmap

Keywords

💡Angle Bisector

An angle bisector is a line that divides an angle into two congruent angles. In the context of the video, the construction of an angle bisector is the primary focus. The script describes the process of drawing a line that cuts an angle into two equal parts, demonstrating the geometric principle that all points on the angle bisector are equidistant from the sides of the angle. This concept is central to the video's theme of geometric construction.

💡Acute Angle

An acute angle is an angle that is less than 90 degrees. The script mentions constructing an acute angle in the middle of the page, which sets the stage for the angle bisector construction. The acute angle serves as the starting point for the demonstration, illustrating the practical application of geometric principles in creating specific angle measurements.

💡Vertex

The vertex of an angle is the point where the two sides of the angle meet. In the script, the angle bisector is said to go through the vertex, which is a necessary step in the construction process. The vertex is the reference point for determining the location of the angle bisector, ensuring that the line drawn will bisect the angle correctly.

💡Compass

A compass is a drafting tool used to draw circles or arcs. In the video script, the compass is used to set the radius that will intersect both sides of the angle, which is a crucial step in finding the point on the angle bisector. The compass allows for precise measurements and ensures that the arcs drawn will intersect at the correct point, demonstrating the importance of tools in geometric construction.

💡Arc

An arc is a segment of the circumference of a circle. The script describes drawing arcs to find the point on the angle bisector. By drawing arcs from the intersections of the sides of the angle and the circle created by the compass, the script illustrates how arcs can be used to locate points equidistant from the sides of the angle, which is essential for constructing the angle bisector.

💡Equidistant

Equidistant means being at an equal distance from two or more points. In the context of the video, the term is used to describe the property of points on the angle bisector, which are equidistant from the sides of the angle. This concept is fundamental to understanding why the constructed line bisects the angle, as it ensures that the two resulting angles are congruent.

💡Straight Edge

A straight edge, also known as a ruler, is a tool used for drawing straight lines. The script mentions using a straight edge to connect the vertex and the new point found on the angle bisector. This action completes the construction by creating the line that bisects the original angle, showcasing the straight edge's role in finalizing geometric constructions.

💡Congruence

Congruence in geometry refers to the property of two figures being identical in shape and size. The script discusses creating two congruent angles as a result of the angle bisector construction. This concept is key to the video's message, as it demonstrates the precision and accuracy achievable through geometric constructions.

💡Construction

In geometry, a construction refers to the process of drawing a figure according to a set of rules. The term is used throughout the script to describe the step-by-step process of creating an angle bisector. The construction process is the main theme of the video, highlighting the methodical approach required to achieve geometric accuracy.

💡Pointer

A pointer is a part of a compass used to mark or draw. The script mentions using the pointer to stab in and draw arcs, which is a part of the process to find the equidistant point on the angle bisector. The pointer is an essential tool in the construction process, enabling the precise drawing of arcs necessary for the angle bisector construction.

💡Intersection

An intersection is a point where two lines, rays, or curves meet. The script describes creating intersections by drawing arcs with a compass, which are then used to find the point on the angle bisector. The concept of intersection is crucial in the construction process, as it helps to identify the correct location for drawing the angle bisector.

Highlights

Introduction to angle bisector construction

Purpose of an angle bisector is to divide an angle into two congruent parts

Construction begins with an acute angle in the center of the page

Angle bisector passes through the vertex and equidistant points on both sides

Using a compass to set the width and intersect both sides of the angle

Drawing arcs to create intersections on both sides of the angle

Using the pointer to draw arcs within the angle from each intersection

Intersection of arcs determines a point equidistant from both sides of the angle

Connecting the vertex to the new point with a straight edge

Resulting in two congruent angles bisected by the line

Explanation of the geometric principle behind the construction

Demonstration of the practical steps in the angle bisector construction

Emphasis on the importance of equidistance for the angle bisector

Visual representation of the construction process

Use of a compass to ensure accurate and consistent measurements

Technique of drawing arcs to find the correct point for the bisector

Final step of connecting the vertex and the equidistant point

Completion of the angle bisector construction