Función inversa | Ejemplo 2
Summary
TLDREste vídeo educativo se centra en el proceso de encontrar la función inversa de una función racional. Se explican los tres pasos clave: verificar la inyectividad de la función, intercambiar variables y despejar la 'y'. Además, se abordan conceptos como dominio y rango, y se ejemplifica el proceso con ejercicios prácticos. El presentador también ofrece un ejercicio para que el espectador practique estos conceptos, subrayando la importancia de la comprensión de las funciones racionales y su inversa.
Takeaways
- 😀 El vídeo es la segunda parte de una serie sobre cómo encontrar la función inversa.
- 🔍 Se explica que una función debe ser inyectiva para tener una función inversa, de lo contrario, se debe restringir su dominio.
- 📚 Se recomienda ver el primer vídeo para comprender mejor las funciones inversas y sus características.
- 📈 Se detalla el proceso de encontrar la función inversa en tres pasos: verificar inyectividad, intercambiar variables y despejar la 'y'.
- 📘 Se discute brevemente el dominio y el rango de una función racional, y cómo estos afectan el dominio y el rango de la función inversa.
- 🧐 Se verifica la inyectividad de la función dada como un paso previo para encontrar su inversa.
- 🔢 Se muestra cómo intercambiar variables y despejar la 'y' para obtener la función inversa.
- 📝 Se enfatiza la importancia de practicar y verificar la función inversa utilizando ejemplos numéricos.
- 📊 Se proporciona un ejercicio similar al tratado en el vídeo para que el espectador pueda practicar y aplicar los conceptos aprendidos.
- ✅ Se recomienda utilizar números que simplifiquen las fracciones y faciliten la verificación de la función inversa.
Q & A
¿Cuál es el objetivo principal del segundo video que se menciona en el guion?
-El objetivo principal es encontrar la función inversa de una función racional específica.
¿Qué tres pasos se deben seguir para encontrar la función inversa de cualquier función?
-Primero, verificar si la función es inyectiva. Segundo, intercambiar las variables. Tercero, despejar la 'y'.
¿Por qué es importante verificar si una función es inyectiva antes de encontrar su inversa?
-Es importante porque si la función no es inyectiva, entonces no tiene función inversa y sería necesario restringir su dominio.
¿Cuál es el dominio de la función racional que se discute en el guion?
-El dominio es todos los números reales excepto -3, ya que el denominador no puede ser cero.
¿Cómo se determina el rango de la función racional en el guion?
-Se observa el numerito que acompaña a la 'x' en la función, y el rango son todos los reales excepto el número que resulta de dividir el numerito superior entre el inferior.
¿Cómo se intercambian las variables para encontrar la función inversa?
-Se reemplaza 'x' con 'y' y 'y' con 'x' en la función original.
¿Qué método se utiliza para verificar si una función es inyectiva según el guion?
-Se verifica si f(x1) = f(x2) implica que x1 = x2, lo que se hace a través de la igualación y manipulación algebraica de las expresiones.
¿Cómo se despeja la 'y' en la función inversa una vez intercambiadas las variables?
-Se multiplica por el denominador para eliminarlo, se aplican las operaciones y se pasa todo lo que tenga la 'y' a un lado y lo que no la tenga a otro, para finalmente factorizar y despejar la 'y'.
¿Cómo se verifica si una función es realmente la inversa de otra?
-Se aplica una función a un número y luego se aplica la inversa al resultado, verificando si se recupera el número original.
¿Qué consejo se da para facilitar los cálculos al verificar la inversa de una función?
-Es recomendable elegir un número que simplifique los cálculos, como uno que haga que el denominador sea uno.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Función inversa | Ejemplo 1 @MatematicasprofeAlex
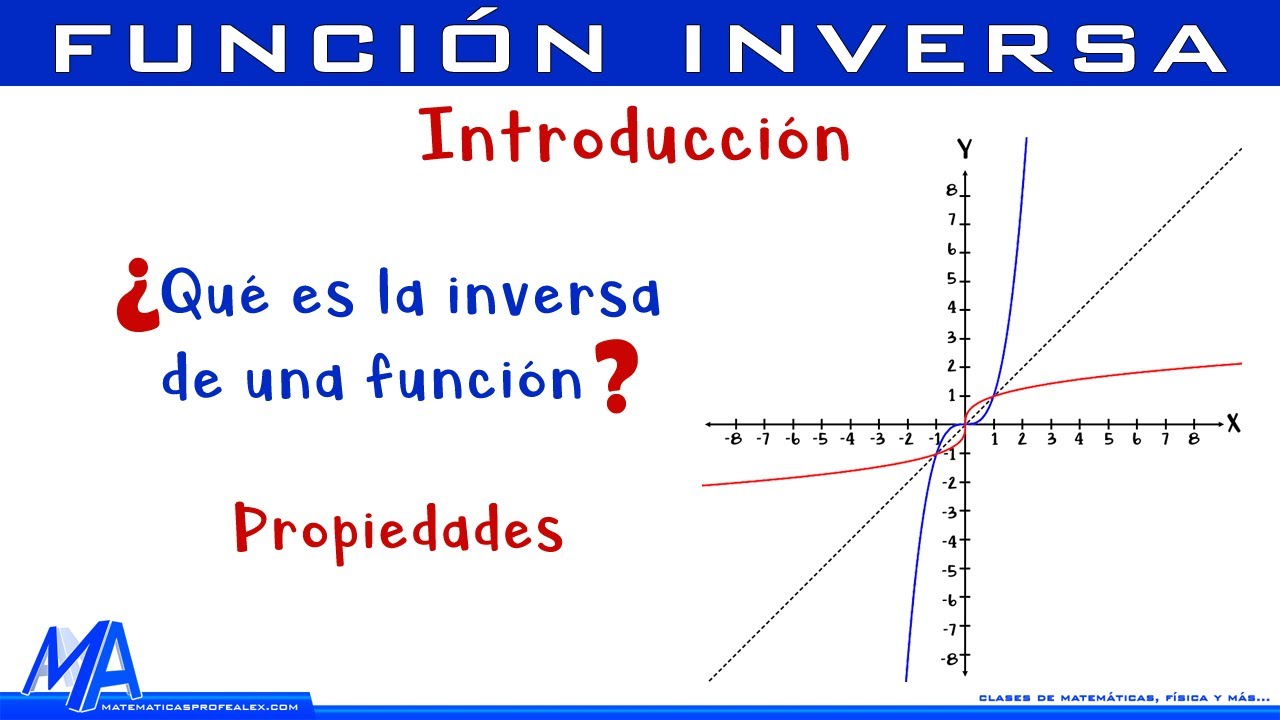
Función inversa | Introducción

Derivada de una función usando la definición | Ejemplo 4
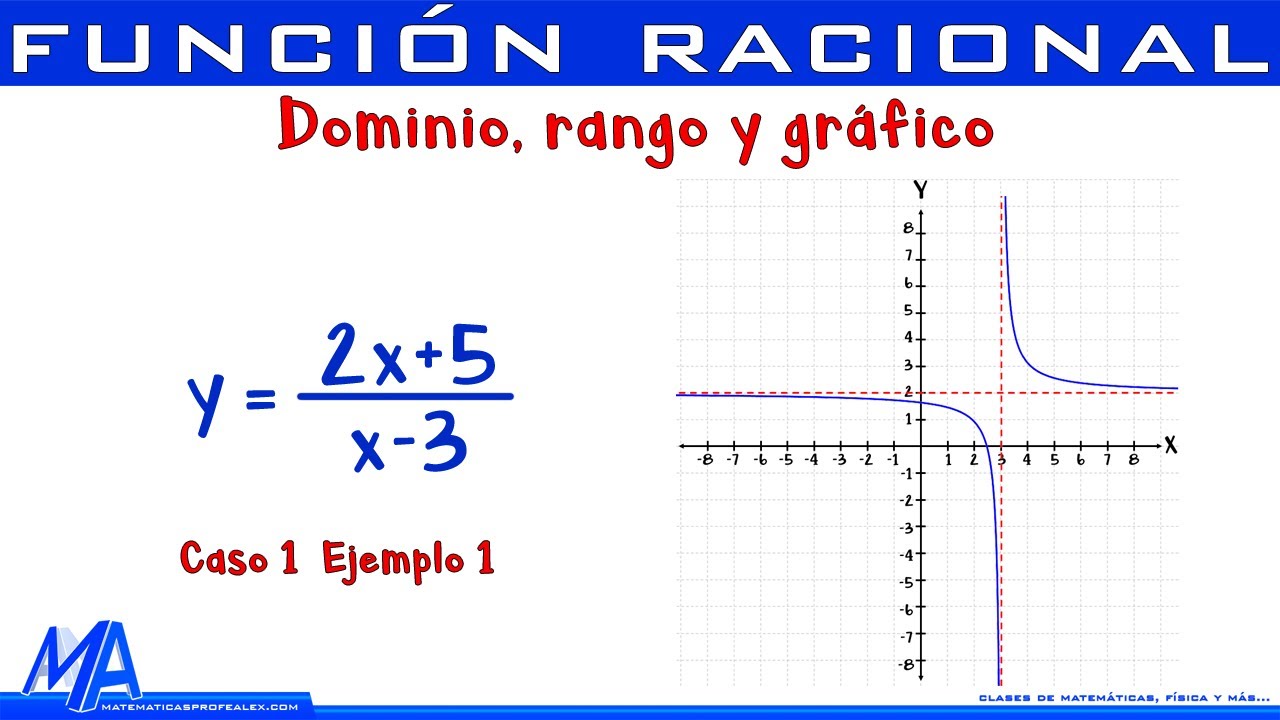
Dominio rango y grafico función Racional | Caso 1 ejemplo 1

Matemáticas - Hallar la pendiente de la recta tangente a una curva + Gráfica.

ASÍNTOTAS VERTICALES y HORIZONTALES 📉 (OBLIGADO VERLO)
5.0 / 5 (0 votes)
