ASÍNTOTAS VERTICALES y HORIZONTALES 📉 (OBLIGADO VERLO)
Summary
TLDREn este video, se explica el proceso para encontrar asíntotas verticales y horizontales de una función racional. Se comienza determinando el dominio de la función mediante la igualación del denominador a cero, lo que revela las asíntotas verticales en x=1 y x=-1. Luego, se estudian los límites laterales para definir el comportamiento en estos puntos. Finalmente, se analiza la presencia de una asíntota horizontal en y=0 al observar el comportamiento de la función cuando x tiende a infinito. Se concluye con un dibujo que representa estas características clave de la función.
Takeaways
- 📐 El dominio de la función es todos los números reales excepto -1 y 1, ya que el denominador se hace cero en esos puntos.
- ⚠️ Hay asíntotas verticales en x = 1 y x = -1 al igualar el denominador a cero.
- 🔢 Para verificar las asíntotas, se evalúan los límites cuando x tiende a 1 y a -1, comprobando que tienden a infinito.
- ↔️ En x = 1, el límite lateral por la izquierda tiende a menos infinito y por la derecha a más infinito.
- 🔄 En x = -1, el límite lateral por la izquierda tiende a menos infinito y por la derecha a más infinito.
- 📊 Los límites laterales ayudan a determinar el comportamiento de la función cerca de las asíntotas.
- ➖ La función tiene una asíntota horizontal en y = 0 porque el límite cuando x tiende a infinito da cero.
- 🧮 La función no tiene asíntotas oblicuas debido a la existencia de la asíntota horizontal.
- ✍️ Se dibujan las asíntotas verticales en x = 1 y x = -1, y la asíntota horizontal en y = 0.
- 🖍️ El gráfico muestra cómo la función se aproxima a menos infinito o más infinito cerca de las asíntotas verticales, sin tocar la asíntota horizontal.
Q & A
¿Qué función se está analizando en el vídeo?
-La función que se analiza es \( f(x) = \frac{14x + 13}{x^2 - 1} \).
¿Cómo se determina el dominio de la función?
-El dominio se determina igualando el denominador a cero, es decir, \( x^2 - 1 = 0 \), lo que da \( x = 1 \) y \( x = -1 \). Por lo tanto, el dominio son todos los reales excepto 1 y -1.
¿Por qué hay asíntotas verticales en \( x = 1 \) y \( x = -1 \)?
-Hay asíntotas verticales en \( x = 1 \) y \( x = -1 \) porque el denominador se iguala a cero en estos valores, lo que produce una tendencia al infinito en la función.
¿Cómo se comprueba la existencia de una asíntota vertical en \( x = 1 \)?
-Se hace el límite cuando \( x \) tiende a 1. Al sustituir en la función, el numerador da 27 y el denominador tiende a 0, lo que da infinito, confirmando la asíntota vertical.
¿Qué sucede cuando \( x \) tiende a 1 por la izquierda y por la derecha?
-Cuando \( x \) tiende a 1 por la izquierda, la función tiende a menos infinito. Cuando \( x \) tiende a 1 por la derecha, la función tiende a más infinito.
¿Cómo se determina el comportamiento en \( x = -1 \) por la izquierda y la derecha?
-Cuando \( x \) tiende a \( -1 \) por la izquierda, la función tiende a menos infinito, y cuando \( x \) tiende a \( -1 \) por la derecha, la función tiende a más infinito.
¿Cómo se identifica si hay una asíntota horizontal?
-Se hace el límite de la función cuando \( x \) tiende a infinito y a menos infinito. Como el grado del denominador es mayor que el del numerador, el límite tiende a 0, indicando una asíntota horizontal en \( y = 0 \).
¿Por qué no hay asíntotas oblicuas en esta función?
-No hay asíntotas oblicuas porque la función tiene una asíntota horizontal en \( y = 0 \), y si existe una asíntota horizontal, no puede haber una oblicua.
¿Qué importancia tiene el análisis de los límites laterales?
-El análisis de los límites laterales es crucial para determinar hacia qué infinito tiende la función cuando se aproxima a los puntos donde hay asíntotas verticales, lo que ayuda a definir el comportamiento gráfico.
¿Qué características clave presenta el gráfico de esta función?
-El gráfico presenta asíntotas verticales en \( x = 1 \) y \( x = -1 \), y una asíntota horizontal en \( y = 0 \). Además, la función tiende a más o menos infinito dependiendo de si se aproxima a las asíntotas verticales por la izquierda o la derecha.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
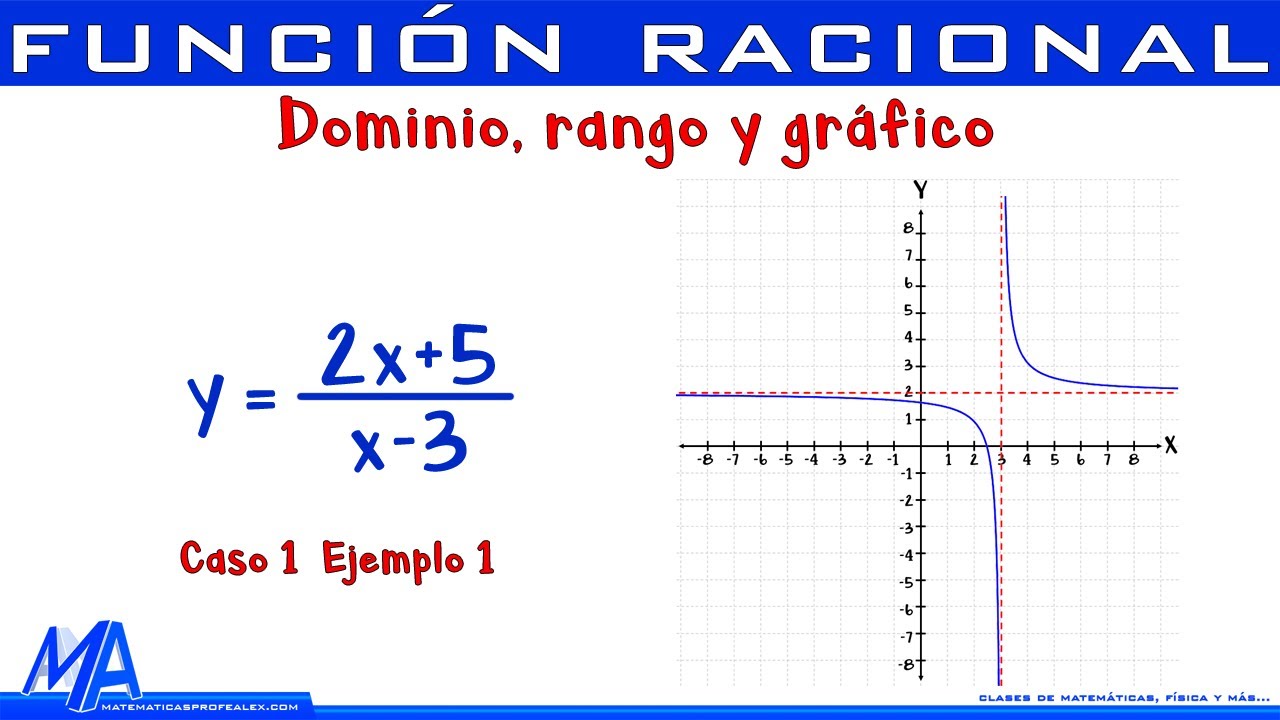
Dominio rango y grafico función Racional | Caso 1 ejemplo 1

Como graficar funciones racionales | Precálculo

Asíntotas verticales, horizontales y oblicuas de una función racional

Función Racional - Ejercicios Nivel 2 - Gráficas

Equilibrio de Cuerpo Rígido, Determinar Reacciones, Estática - Salvador FI

CONSTRUCCIÓN DE CILÍNDROS 2023
5.0 / 5 (0 votes)
