Matematika SMA - Barisan dan Deret (1) - Barisan Aritmatika, Rumus Barisan Aritmatika (A)

Summary

This educational video script focuses on arithmetic sequences, providing a comprehensive guide from basic concepts to advanced problem-solving. It explains the definition of arithmetic sequences, the formula to find the common difference, and how to calculate the nth term. The script includes several examples and exercises to illustrate the process of determining specific terms within a sequence. It also covers how to find the number of terms and solve for 'n' when given certain sequence terms. The video aims to make learning arithmetic sequences accessible and engaging for viewers.

Takeaways

• 📚 The video is an educational tutorial focused on arithmetic sequences, providing a comprehensive understanding of the topic.
• 🔢 Arithmetic sequences are defined as series where the difference between any two consecutive terms is constant.
• 📈 The script includes examples of arithmetic sequences, such as 2, 5, 8, 11, and explains how to identify the common difference.
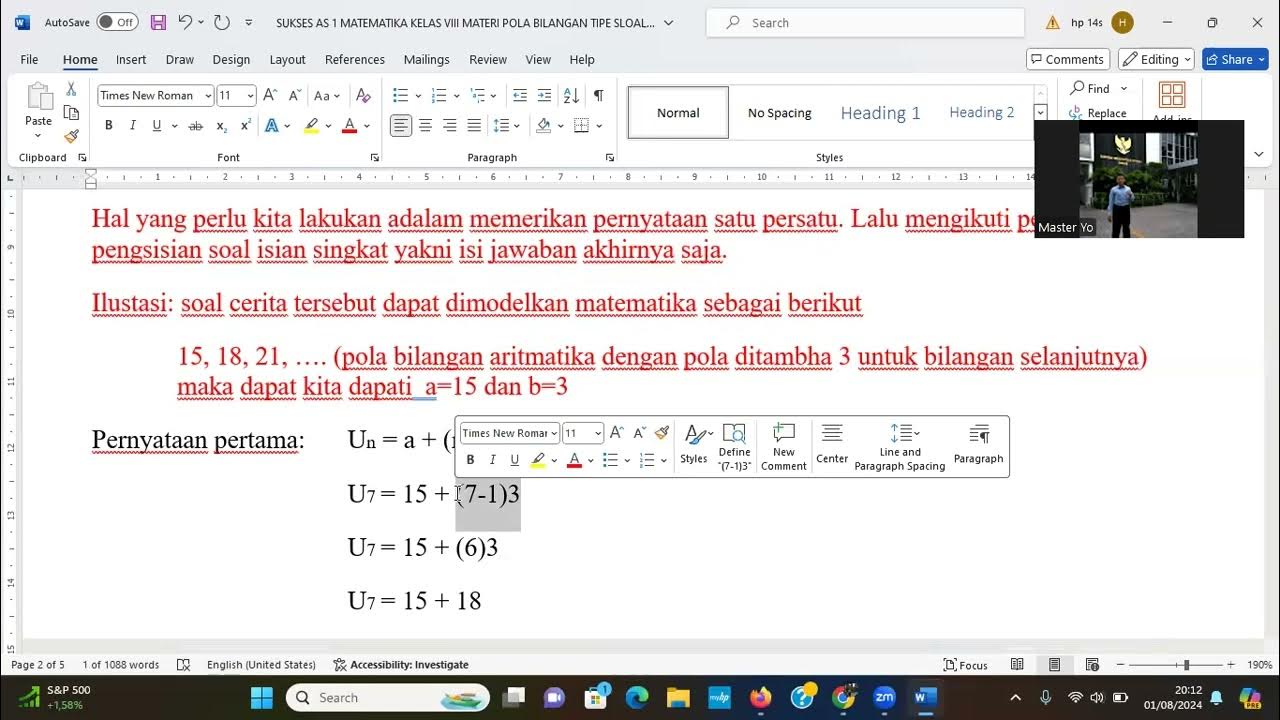
• 📝 The formula to find the nth term of an arithmetic sequence is introduced as "U_n = a + (n-1)b", where "a" is the first term and "b" is the common difference.
• 📑 The tutorial walks through solving exercises to find specific terms in arithmetic sequences, using the provided formulas.
• 🧮 The video demonstrates how to calculate the 15th term for different arithmetic sequences by substituting values into the nth term formula.
• 🔍 The process of finding the first term and the common difference when given the 4th and 9th terms of a sequence is explained.
• 📐 The script includes a problem-solving approach where the terms of a sequence are converted into fractions to identify the common difference.
• 🔑 The video shows how to determine the position in the sequence (n) when the sequence is given in fractional form and a specific term is known.
• 🎯 The tutorial concludes with a problem involving finding the number of terms in a sequence that are divisible by 3 within a given range, demonstrating the application of arithmetic sequence concepts.

Q & A

What is the definition of an arithmetic sequence mentioned in the script?

An arithmetic sequence is defined as a series that has the same difference between any two consecutive terms.

What is the formula used to find the common difference in an arithmetic sequence?

The formula used to find the common difference is \( U_{n+1} - U_n \), where \( U_n \) is a term in the sequence.

How do you calculate the nth term of an arithmetic sequence as described in the script?

The nth term of an arithmetic sequence can be calculated using the formula \( U_n = a + (n-1)b \), where \( a \) is the first term and \( b \) is the common difference.

What is the example given in the script for the first term and the common difference in an arithmetic sequence?

The example given is the sequence 2, 5, 8, 11, where the first term \( a \) is 2 and the common difference \( b \) is 3.

How is the 15th term of a sequence calculated in the script for point A?

For point A, the 15th term is calculated by substituting \( n = 15 \) into the given formula \( u_n \), resulting in the term being 41.

What is the method to determine the 15th term for point B in the script?

For point B, the 15th term is found by using the formula \( u_{15} = 15 - 3 \times 15 = -30 \).

What is the approach to find the 15th term in point C of the arithmetic sequence?

In point C, the first term \( a \) is identified as 6 and the common difference \( b \) as 4. The 15th term is then calculated using \( u_{15} = 6 + 14 \times 4 = 62 \).

How is the 15th term of the sequence in point D determined according to the script?

For point D, the first term \( a \) is 4 and the common difference \( b \) is -3. The 15th term is calculated as \( u_{15} = 4 + 14 \times (-3) = -38 \).

What is the method used in the script to find the 7th term of an arithmetic sequence given the 4th and 9th terms?

The method involves using the known terms to find the common difference and then applying the formula for the nth term to find the 7th term, which is calculated to be 29.

How does the script simplify the arithmetic sequence with fractions to find the value of n?

The script simplifies the sequence by converting all terms to have a common denominator, then observes the numerators form an arithmetic sequence, and uses this to find the value of n.

What is the strategy to find the number of terms divisible by 3 between 1 and 500 as described in the script?

The strategy involves identifying the first term, common difference, and the last term of the arithmetic sequence formed by numbers divisible by 3, then using the formula for the nth term to find the number of terms.