Trigonometric Fourier Series
Summary
TLDRThis lecture delves into trigonometric Fourier series expansion, crucial for analyzing periodic signals. It explains the derivation of coefficients: a₀ (DC value), an, and bn, which are integral for reconstructing the signal. The lecture highlights the simplifications in calculating these coefficients based on signal properties like symmetry and even-odd characteristics. Practical examples, including a rectangular wave, illustrate the application of these concepts, with further exercises provided for practice.
Please replace the link and try again.
Q & A
What are the three types of Fourier series expansion mentioned in the script?
-The three types of Fourier series expansion mentioned are trigonometric Fourier series, complex exponential or simply exponential Fourier series, and polar or harmonic Fourier series.
For what kind of signals is Fourier series expansion applicable?
-Fourier series expansion is applicable only for periodic signals. Non-periodic signals cannot have a Fourier series expansion.
What is the mathematical representation of a periodic signal using trigonometric Fourier series expansion?
-A periodic signal XT can be represented as the sum of its DC or average value (a sub zero), all the cosine terms (a n times cos(Omega naught T)), and all the sine terms (B n times sin(Omega naught T)), where the summation for both cosine and sine terms is from 1 to infinity.
How is the DC or average value of a periodic signal calculated?
-The DC or average value (a naught) is calculated by finding the total area under the signal in one time period and then dividing it by the fundamental time period.
What are the formulas for calculating the Fourier coefficients a n and B n?
-The Fourier coefficient a n is calculated by integrating the product of the signal XT and 2 cos(n Omega naught T) over one fundamental time period, divided by T naught. The coefficient B n is calculated similarly, but with the product of the signal XT and 2 sin(n Omega naught T).
What is the significance of the coefficients a n and B n in the Fourier series expansion?
-The coefficients a n and B n represent the weights of the cosine and sine terms respectively in the Fourier series expansion. They indicate the contribution of each harmonic to the overall signal.
Why might it be unnecessary to calculate a naught for a given signal?
-It is unnecessary to calculate a naught if the signal is symmetrical about the time axis, as this implies the average or DC value will be zero.
Under what condition would the coefficient B n be equal to zero?
-The coefficient B n would be equal to zero if the given periodic signal is an even signal, meaning it remains the same after time reversal.
What is the condition for a signal to be considered odd, and how does this affect the coefficients?
-A signal is considered odd if it becomes the negative of itself after time reversal. For odd signals, the coefficient a n is equal to zero, and there is no need to calculate it.
What is the practical implication of the script's discussion on calculating Fourier coefficients for different types of signals?
-The discussion on calculating Fourier coefficients helps in understanding when certain coefficients can be assumed to be zero based on signal properties, thus saving time and computational effort in Fourier series analysis.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
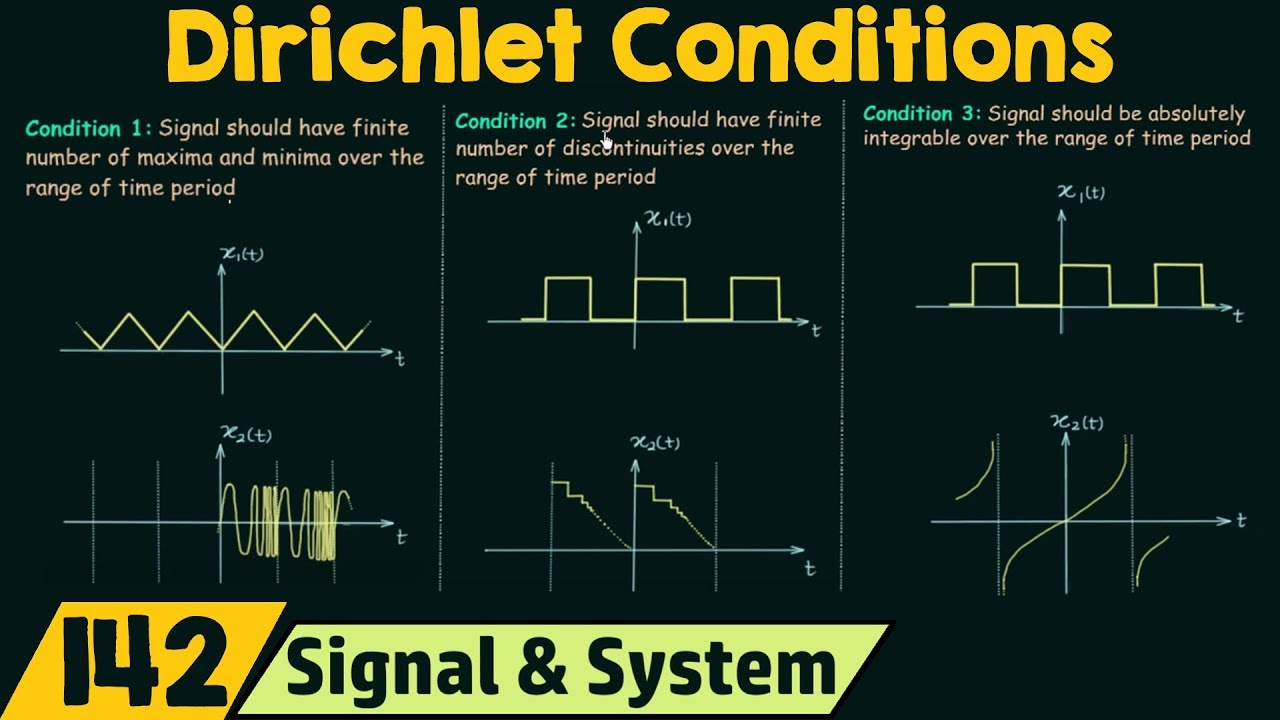
Conditions for Existence of Fourier Series (Dirichlet Conditions)

Introduction to Fourier Series | Trigonometric Fourier Series Explained
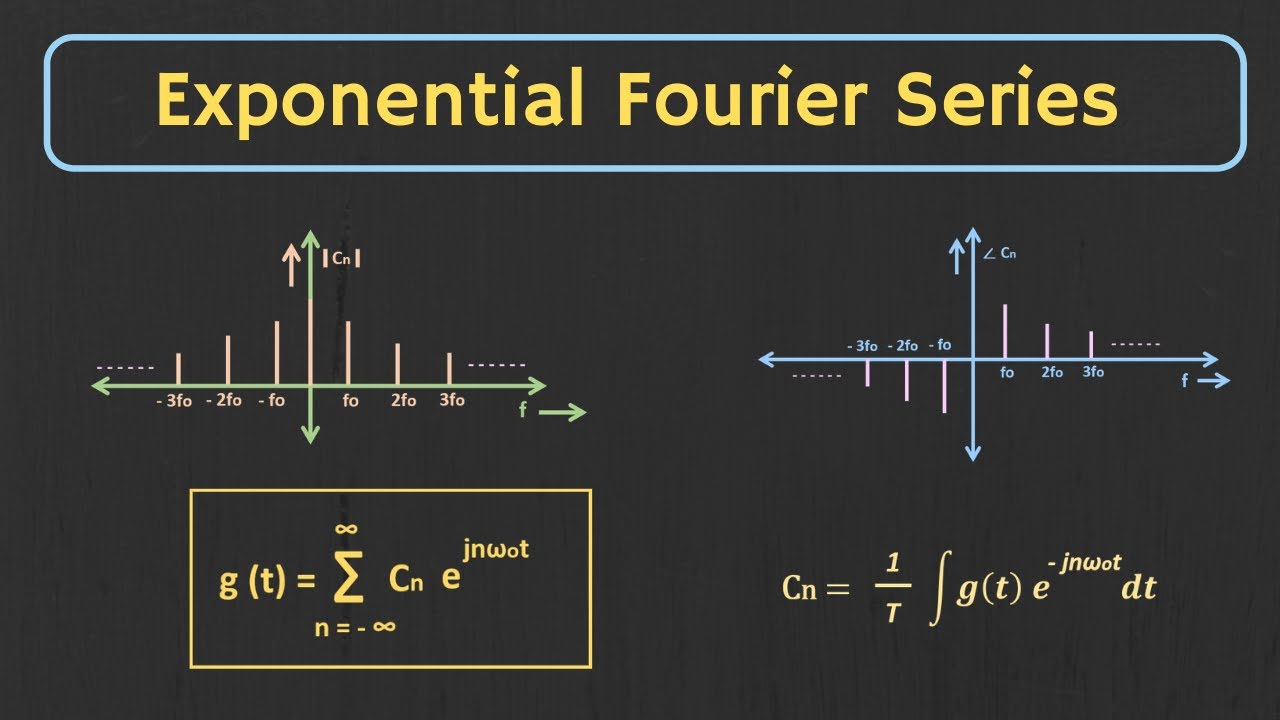
Exponential Fourier Series Explained | Concept of Negative Frequency Explained
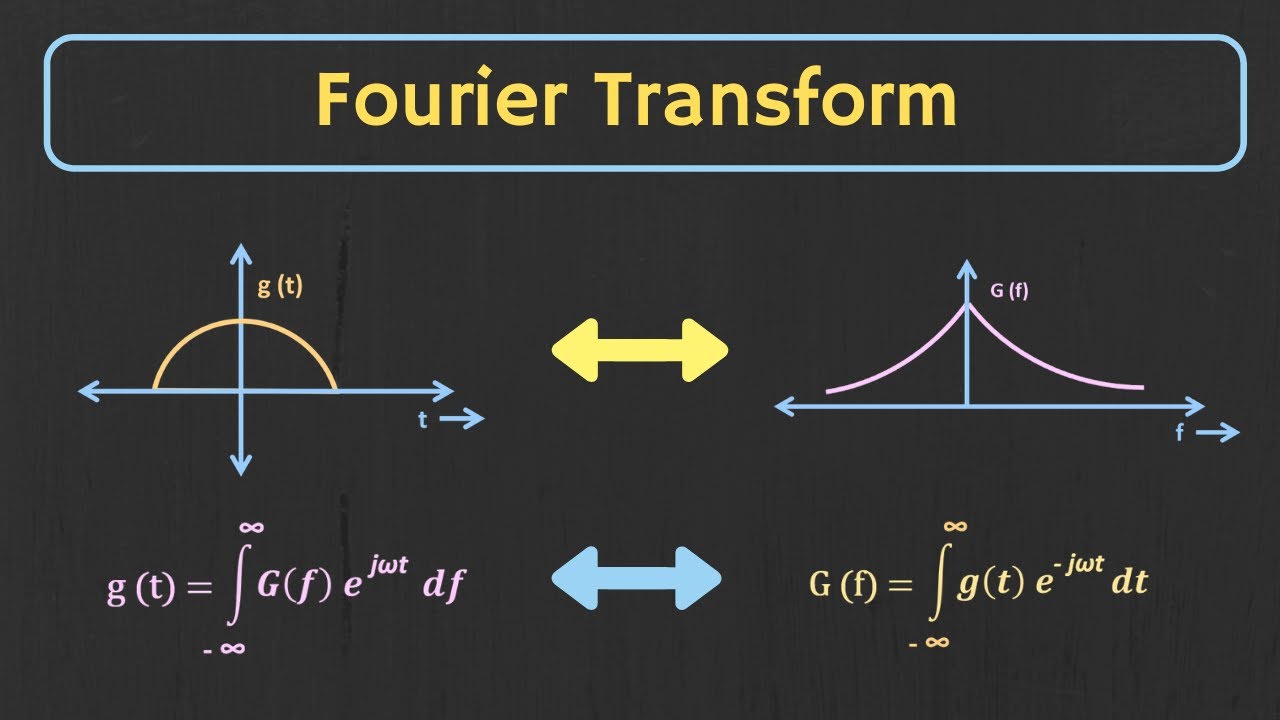
Fourier Transform Explained

FOURIER SERIES LECTURE 1 | STUDY OF DEFINITION AND ALL BASIC POINTS @TIKLESACADEMY

U5_L1_Basics of Signal representation and Analysis | Electronics Engineering (BEC101/201)| Hindi
5.0 / 5 (0 votes)