Solving Quadratic Equation Using Quadratic Formula
Summary
TLDRThis educational video script delves into solving quadratic equations using the quadratic formula. It guides viewers step-by-step through the process of rewriting equations in standard form, identifying coefficients, applying the formula, and verifying solutions. The script includes three examples, illustrating the method's application and emphasizing the importance of checking solutions against the original equation for accuracy.
Takeaways
- 📚 The script discusses the quadratic formula as a method for solving quadratic equations.
- 🔍 The quadratic formula is derived from the standard form of a quadratic equation by completing the square.
- 📝 The standard form of a quadratic equation is \( ax^2 + bx + c = 0 \).
- 📈 The quadratic formula is expressed as \( x = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a} \).
- ✍️ To use the quadratic formula, first rewrite the equation in the standard form to identify values of \( a \), \( b \), and \( c \).
- 🔢 Substitute the identified values into the quadratic formula to find the solutions for \( x \).
- 📉 The script provides a step-by-step guide to solving quadratic equations using the quadratic formula.
- 📝 Example problems are given to demonstrate the application of the quadratic formula in solving equations.
- 🔍 The script emphasizes the importance of checking the solutions obtained by substituting them back into the original equation.
- 🔗 The solutions to a quadratic equation can be real numbers, and in some cases, they may be the same, indicating a repeated root.
- 👩🏫 The lesson is presented by a teacher named Michela, who guides the viewers through the process of solving quadratic equations.
Q & A
What is the quadratic formula used for?
-The quadratic formula is used for solving quadratic equations of the form ax^2 + bx + c = 0.
How is the quadratic formula derived?
-The quadratic formula is derived by completing the square from the standard form of a quadratic equation.
What does the quadratic formula represent?
-The quadratic formula is represented as x = (-b ± √(b^2 - 4ac)) / (2a), where x is the solution to the quadratic equation.
What are the steps to solve a quadratic equation using the quadratic formula?
-The steps are: 1) Write the equation in the form ax^2 + bx + c = 0, 2) Identify the values of a, b, and c, 3) Substitute these values into the quadratic formula, and 4) Simplify to find the solutions.
What is the significance of the discriminant in the quadratic formula?
-The discriminant (b^2 - 4ac) determines the nature of the roots of the quadratic equation. If it's positive, there are two real roots; if zero, one real root; and if negative, two complex roots.
How do you rewrite the equation x^2 + 5x = 14 in the standard form for the quadratic formula?
-You rewrite it as x^2 + 5x - 14 = 0 by subtracting 14 from both sides of the equation.
What are the values of a, b, and c for the equation x^2 + 5x = 14 after rewriting it in standard form?
-The values are a = 1, b = 5, and c = -14.
What are the solutions to the equation x^2 + 5x = 14 using the quadratic formula?
-The solutions are x = 2 and x = -7.
How do you verify the solutions to a quadratic equation?
-You substitute the solutions back into the original equation to see if both sides of the equation are equal.
What is the difference between the solutions x = 2 and x = -7 for the equation x^2 + 5x = 14?
-The difference is that they are the two distinct real roots of the equation, which are found using the quadratic formula.
What is the equation 3x^2 - x + 5 = 7 rewritten in the standard form for the quadratic formula?
-The equation is rewritten as 3x^2 - x - 2 = 0 after subtracting 7 from both sides.
What are the solutions to the equation 3x^2 - x + 5 = 7 using the quadratic formula?
-The solutions are x = 1 and x = -2/3.
How many distinct solutions does the equation x^2 + 2x + 1 = 0 have?
-The equation has only one distinct solution, which is x = -1, because the discriminant is zero.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Solving Equations Transformable into Quadratic Equations

Solving Quadratic Equations

Persamaan Kuadrat Kelas 10 Kurikulum Merdeka
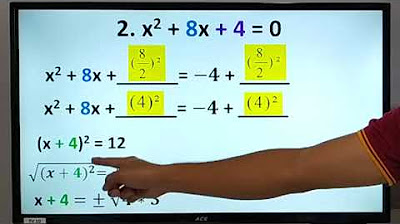
Math8 1G LV4 - Completing the Square and Quadratic Formula

Maths - EB11 - S - chap2 - v1 - polynomes et equation du second degre

Persamaan Kuadrat •Part 1: Menyelesaikan Persamaan Kuadrat dengan Pemfaktoran / Faktorisasi Tipe 1&2
5.0 / 5 (0 votes)