Elementary flows [Aerodynamics #9]
Summary
TLDRThis lecture delves into incompressible and inviscid aerodynamics, focusing on irrotational flows and Bernoulli's equation. It introduces elementary flows as building blocks for complex aerodynamic analyses, covering uniform flow, source/sink, doublet, and vortex. The script explains how to construct these flows analytically using stream functions and velocity potentials, and demonstrates creating aerodynamic flow fields for bodies like the semi-infinite body, Rankine oval, stationary, and rotating cylinders. It concludes with practical applications in computational fluid dynamics, highlighting source and vortex panel methods.
Takeaways
- 📚 The lecture focuses on incompressible and inviscid flows, introducing the Bernoulli equation and the Laplace equation for velocity potential and stream function.
- 🌀 The concept of irrotationality allows for the application of Bernoulli's equation universally if the flow is irrotational, and both velocity potential and stream function satisfy the Laplace equation.
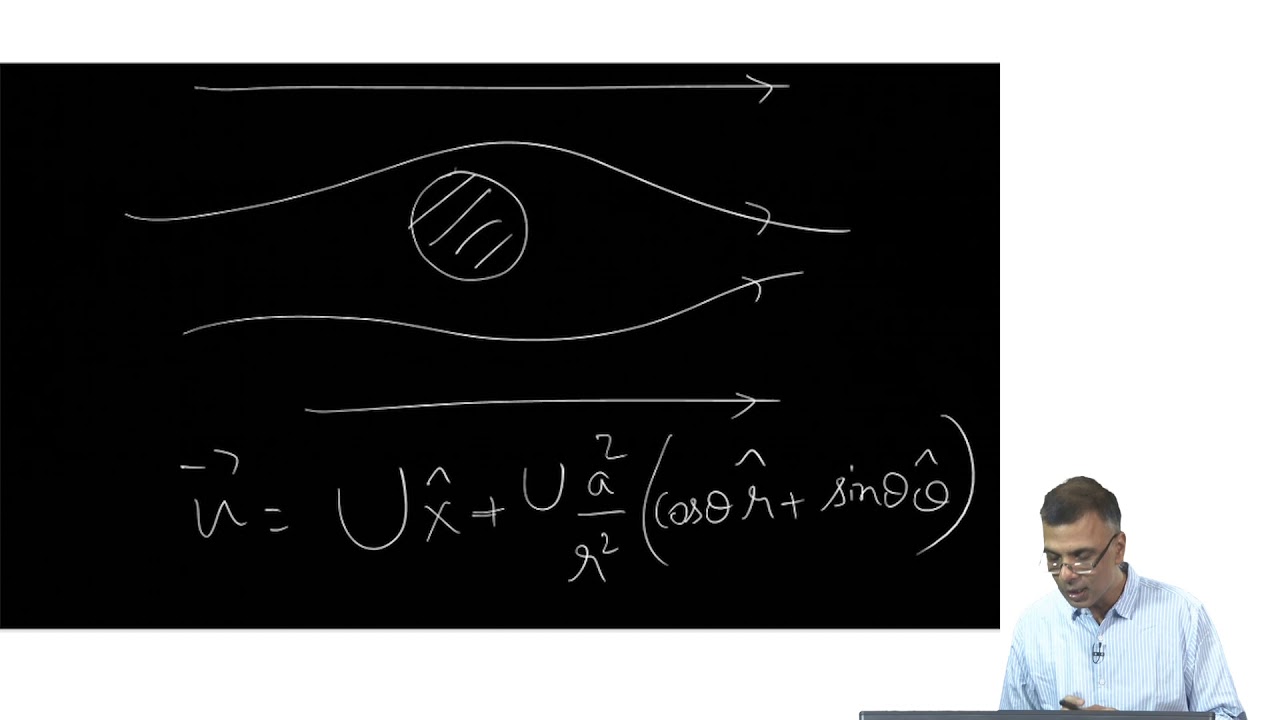
- 🏗️ Elementary flows are the building blocks of aerodynamics, including the uniform flow, source and sink, doublet, and vortex, which can be combined to model more complex flows.
- 🔍 The Laplace equation's linearity allows for the superposition of solutions, meaning different elemental flows can be added together to describe more complex flow patterns.
- 💡 Inviscid flow does not have boundary layers, eliminating the no-slip condition and allowing fluid to move freely without viscosity affecting its motion.
- 📐 Cylindrical coordinates are used predominantly in the lecture due to the round nature of many elementary flows, making it a more natural choice than Cartesian coordinates.
- 🌊 The uniform flow represents translational movement and is a fundamental component in constructing other flow models.
- 💧 Sources and sinks are opposite flows characterized by streamlines that emit outwards or inwards from a single point, with their strength defined by the volumetric flow rate per unit span.
- 🔗 The doublet is formed by combining a source and a sink very close together, with its strength defined by the constant product of lambda and the separation distance as the distance approaches zero.
- 🌀 The vortex flow is characterized by fluid orbiting a central point, with no radial velocity and a constant angular velocity, and its strength is defined by circulation.
- 🛠️ The lecture demonstrates constructing more complex flows such as the semi-infinite body, Rankine oval, stationary cylinder, and rotating cylinder using the elemental flows as building blocks.
- 🔧 Computational Fluid Dynamics (CFD) commonly utilizes these elementary flows in flow-solving techniques, such as source panel and vortex panel methods for modeling flow around bodies.
Q & A
What are the two main equations in the field of incompressible and inviscid flows?
-The two main equations are the Bernoulli equation, which relates pressure and velocity along a streamline, and the Laplace equation, which is satisfied by both the velocity potential and the stream function if the flow is irrotational.
Why is the Bernoulli equation applicable everywhere if the flow is irrotational?
-The Bernoulli equation is applicable everywhere in an irrotational flow because the flow's properties can be described by a velocity potential, which is a scalar quantity that satisfies the Laplace equation, allowing for the conservation of mechanical energy along a streamline.
What is the significance of being able to add solutions of the Laplace equation together?
-The ability to add solutions of the Laplace equation together is significant because it allows for the creation of complex flow fields by superimposing multiple elemental flows, each with its own stream function and velocity potential.
What are the four main elementary flows covered in the lecture?
-The four main elementary flows are the uniform flow, the source and sink, the doublet, and the vortex.
How does the absence of boundary layers in inviscid flow affect the fluid movement over surfaces?
-In inviscid flow, the absence of boundary layers means that there is no viscosity to slow down the fluid, and there is no no-slip condition to consider, allowing the fluid to move freely over surfaces.
What is the definition of a source and sink in the context of elementary flows?
-A source and sink are elementary flows characterized by streamlines that emit outwards (source) or inwards (sink) from a single point. They are identical in nature but opposite in direction, with the source having a positive volumetric flow rate and the sink having a negative one.
How is the stream function for a source or sink constructed in cylindrical coordinates?
-The stream function for a source or sink in cylindrical coordinates is constructed by using the radial velocity, which is the volumetric flow rate divided by the local circumference (2πr), and setting the azimuthal velocity to zero. The stream function is then expressed as a function of r and θ, with the sign depending on whether it is a source or sink.
What is the concept of a doublet in elementary flows, and how is it created?
-A doublet is created by combining a source and a sink with equal and opposite strengths that are placed very close together. As the distance between them approaches zero and the product of the distance and the flow rate remains constant, the doublet is formed, characterized by a strength parameter k or kappa.
How is the vortex flow characterized in terms of its velocity field?
-The vortex flow is characterized by having no radial velocity and a constant angular velocity, defined by the circulation divided by 2π. It represents fluid orbiting around a central point, with the flow being irrotational everywhere except at the center.
What is the practical application of elementary flows in computational fluid dynamics (CFD)?
-In CFD, elementary flows are commonly used in flow solving techniques such as the source panel method for non-lifting bodies and the vortex panel method for lifting bodies. These methods involve defining the surface of a body as a series of sources or vortices and using stream functions to recreate the boundary of the body.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
mod03lec11 - Recap - Potential flows, Bernoulli constant and its applications

MekFlu #1: Prinsip Persamaan Bernoulli

Rotational and irrotational flow [Aerodynamics #7]
Mekanika Fluida FM01 (Lecture3: 3/8). Pressure across streamline

Mekanika Fluida FM01 (Lecture3: 7/8). Static-Pitot Tube
Fluidos Ideais em Movimento parte I
5.0 / 5 (0 votes)
