Mekanika Fluida FM01 (Lecture3: 7/8). Static-Pitot Tube
Summary
TLDRThis video explores Bernoulli's principle, explaining how it relates to fluid dynamics, specifically in terms of pressure, velocity, and energy in a streamline. It emphasizes the assumptions behind Bernoulli's equation, such as incompressible fluids and the absence of friction. The speaker also delves into practical applications, like using a venturi meter to calculate flow velocity. Furthermore, the principle is linked to real-world systems such as commercial aircraft. The video also discusses how static and dynamic pressures contribute to fluid behavior and provides insights on how these concepts are applied in various engineering fields.
Takeaways
- 😀 Bernoulli's principle relates the changes in hydrodynamic quantities like pressure and velocity along a streamline.
- 😀 The principle assumes the fluid is non-viscous and incompressible, meaning it doesn't account for friction or significant density changes.
- 😀 Bernoulli's equation can be applied to liquids like water, oil, and sometimes air, provided the airspeed is low enough for the assumptions to hold.
- 😀 Fluid flow must remain along the same streamline for Bernoulli's equation to apply. If the flow crosses streamlines, different equations are needed.
- 😀 The Venturi meter is used to measure the speed of fluid in a pipe by utilizing the change in pressure and cross-sectional area of the pipe.
- 😀 A manometer is used to measure the pressure difference caused by changes in velocity in a venturi tube, where one side has fluid of lower density.
- 😀 Stagnation points occur where the fluid velocity becomes zero, resulting in higher pressure at those points.
- 😀 Bernoulli's equation helps derive the fluid velocity by balancing static and dynamic pressures in a flow system.
- 😀 In applying Bernoulli's equation, the relationship between the static pressure, dynamic pressure, and fluid velocity is fundamental for calculations.
- 😀 The final equation for fluid velocity involves both the density of the fluid and the pressure difference, which can be used in practical applications like calculating airflow in airplanes.
Q & A
What is Bernoulli's principle used for?
-Bernoulli's principle helps in understanding the relationship between changes in hydrodynamic quantities, like pressure and velocity, within a streamline, often used in fluid dynamics.
What are the main assumptions made when applying Bernoulli's principle?
-The three main assumptions are: the fluid is incompressible, the flow is non-viscous, and the flow is along a streamline.
Why is Bernoulli's principle not applicable for viscous fluids?
-Bernoulli's principle assumes no frictional forces (viscosity) in the fluid. Viscous fluids introduce friction, which is not considered in the Bernoulli equation.
What type of fluids can Bernoulli's equation be applied to?
-Bernoulli's equation can be applied to incompressible fluids like liquids (water, oil) and sometimes low-speed gases, assuming the flow is non-viscous.
What is the role of a venturimeter in fluid flow measurement?
-A venturimeter is used to measure the velocity of fluid flowing through a pipe by utilizing changes in pressure as the fluid passes through a constricted section.
What is the principle behind a manometer used in Bernoulli's application?
-A manometer measures the pressure difference between two points in a fluid. It helps calculate the velocity of the fluid by assessing the pressure difference.
How does the principle of hydrostatics relate to Bernoulli's equation?
-Hydrostatics is used in Bernoulli’s principle to calculate the pressure difference in fluids due to changes in elevation. It states that pressure increases as depth increases in a fluid.
Why is the velocity zero at the stagnation point in a flow?
-At the stagnation point, the incoming fluid velocity becomes zero because the flow is brought to rest as it directly impacts a surface that is perpendicular to the flow.
What does the equation for velocity derived from Bernoulli's principle represent?
-The derived velocity equation from Bernoulli's principle represents the speed of the fluid at one point in a streamline, based on pressure differences between two points in the fluid flow.
How is Bernoulli’s equation applied in commercial aircraft?
-In commercial aircraft, Bernoulli’s equation is applied using devices like pitot tubes to measure airspeed, as pressure differences between static and dynamic pressures can determine the velocity of the airflow.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

P bahri
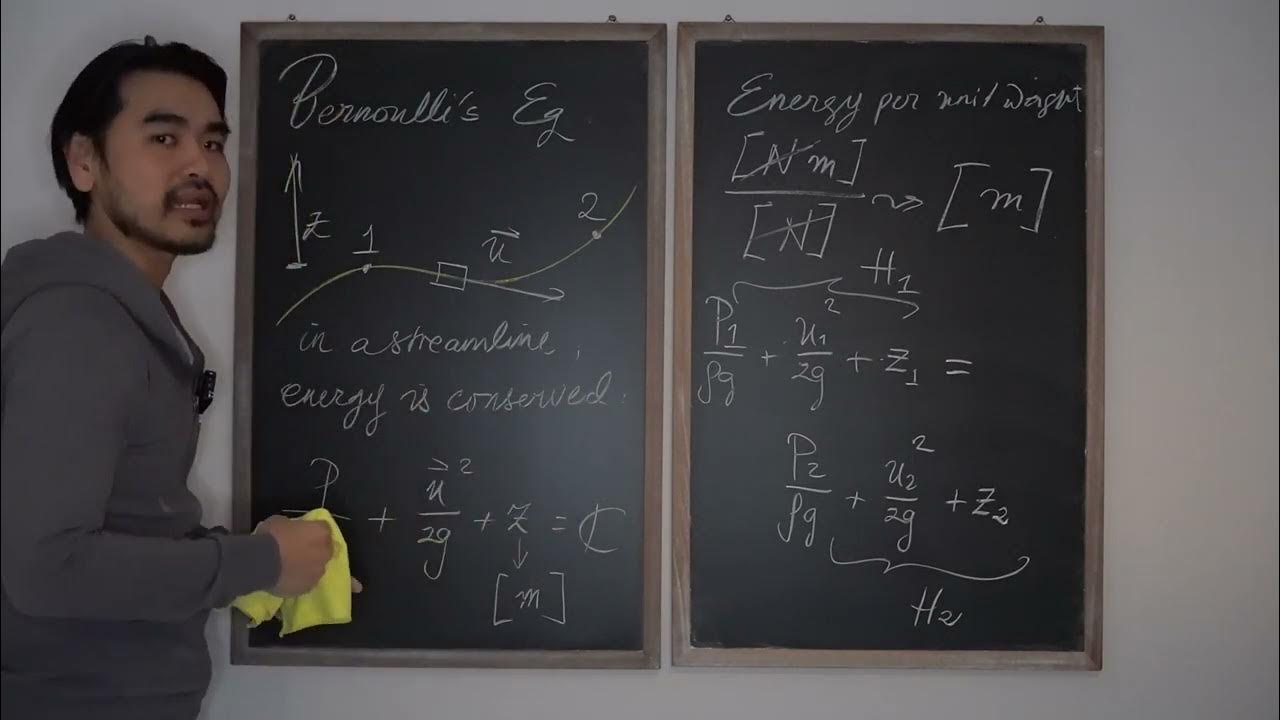
Mekanika Fluida FM01 (Lecture3: 1/8). Persamaan Bernoulli (Pengenalan)

MekFlu #1: Prinsip Persamaan Bernoulli

Fluida Dinamis - Konsep Bernoulli - Simple Konsep - Fisika Kelas 11

Mekanika Fluida FM01 (Lecture3: 8/8). Energy Line & Hydraulic Grade Line
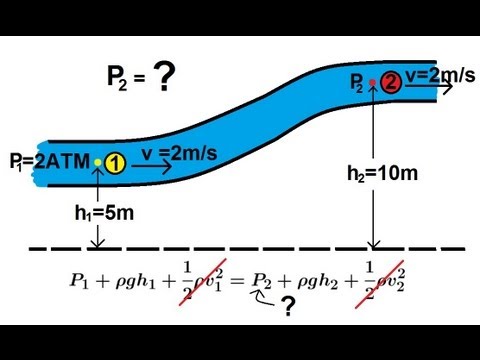
Physics 34 Fluid Dynamics (1 of 7) Bernoulli's Equation
5.0 / 5 (0 votes)