tamaño de la muestra de una población finita
Summary
TLDREn esta clase, se explica cómo calcular el tamaño de una muestra para una población finita. El profesor, un alumno del c04, utiliza un ejemplo práctico para demostrar el proceso. Se introducen conceptos como la confiabilidad (Z), la probabilidad a favor (p) y en contra (q), y el error de estimación (e). Para una población de 4420 individuos y un nivel de confiabilidad del 95%, se aplica una fórmula que considera estos valores para determinar que se necesitan 529 personas en la muestra. Este método es crucial para realizar encuestas y estudios con una alta precisión y confiabilidad.
Takeaways
- 📚 La clase trata sobre cómo calcular el tamaño de una muestra en una población finita.
- 🔍 El tamaño de la muestra (n) es la variable a calcular, mientras que el tamaño de la población (N) es un dato conocido.
- 📈 Se utiliza un nivel de confianza (Z) para determinar la precisión de la encuesta, en este caso, 95% de confiabilidad.
- 📊 La probabilidad a favor (p) y la probabilidad en contra (q) se consideran iguales, cada una con un valor de 0.5.
- 🧮 El error de estimación (e) se divide por 100 y tiene un valor de 0.4 en este ejemplo.
- 🔢 Se utiliza una fórmula específica que incluye Z, p, q y e para calcular el tamaño de la muestra.
- 📐 Se despeja la fórmula con los valores dados y se realizan operaciones matemáticas para obtener el resultado.
- 📉 El cálculo resulta en una división que proporciona un valor aproximado de 528.96, redondeado a 529.
- 🎯 Para alcanzar un 95% de confiabilidad en una encuesta de una población de 4420, se recomienda encuestar a 529 personas.
- ✅ El cálculo garantiza que la información recolectada tenga una alta precisión y confiabilidad.
Q & A
¿Qué es el tamaño de la muestra en un estudio estadístico?
-El tamaño de la muestra es el número de individuos o elementos que se seleccionan de una población para realizar un análisis estadístico representativo.
¿Cuál es la relación entre el tamaño de la muestra y el tamaño de la población en el ejemplo proporcionado?
-En el ejemplo, el tamaño de la población es de 4420 individuos y se busca determinar el tamaño de la muestra necesaria para obtener un nivel de confiabilidad deseado.
¿Qué significa 'n' minúscula y 'N' mayúscula en el contexto del ejemplo?
-En el ejemplo, 'n' minúscula se refiere al tamaño de la muestra (la incógnita que se busca), mientras que 'N' mayúscula representa el tamaño total de la población.
¿Qué es el nivel de confiabilidad 'Z' y cómo se determina?
-El nivel de confiabilidad 'Z' es un valor que indica el grado de confianza que se tiene en los resultados de un estudio estadístico. En el ejemplo, se utiliza una tabla de estadística para determinar que 'Z' para un 95% de confiabilidad es 1.96.
¿Cómo se calculan las probabilidades 'p' y 'q' en el estudio?
-Las probabilidades 'p' (a favor) y 'q' (en contra) se calculan como porcentajes y se dividen entre 100 para adaptarlas a la fórmula de cálculo del tamaño de la muestra.
¿Qué representa la letra 'e' en el contexto del ejemplo?
-La letra 'e' representa el error de estimación en el estudio, que es el margen de error aceptable en los resultados del estudio. En el ejemplo, 'e' se divide entre 100 y tiene un valor de 0.4.
¿Cuál es la fórmula utilizada para calcular el tamaño de la muestra en el ejemplo?
-La fórmula utilizada en el ejemplo no se menciona explícitamente en el guion, pero se basa en la sustitución de valores de 'Z', 'p', 'q' y 'e' en una ecuación estándar para calcular el tamaño de la muestra.
¿Cómo se obtiene el resultado final del tamaño de la muestra en el ejemplo?
-Después de sustituir los valores en la fórmula y realizar los cálculos, se obtiene un resultado de 528.96, que se redondea a 529. Esto significa que se necesitan 529 individuos en la muestra para alcanzar el nivel de confiabilidad deseado.
¿Cuál es el nivel de confiabilidad que se busca en el estudio de ejemplo?
-El nivel de confiabilidad buscado en el estudio de ejemplo es del 95%, lo que indica una alta confianza en los resultados del estudio.
¿Cómo se relaciona el tamaño de la muestra con el error de estimación?
-Un tamaño de muestra más grande generalmente reduce el error de estimación, ya que se tiene más información para hacer inferencias acerca de la población completa.
¿Por qué es importante determinar el tamaño de la muestra adecuadamente?
-Determinar el tamaño de la muestra adecuadamente es crucial para garantizar que los resultados del estudio sean representativos y confiables, evitando costos innecesarios y errores en la toma de decisiones.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
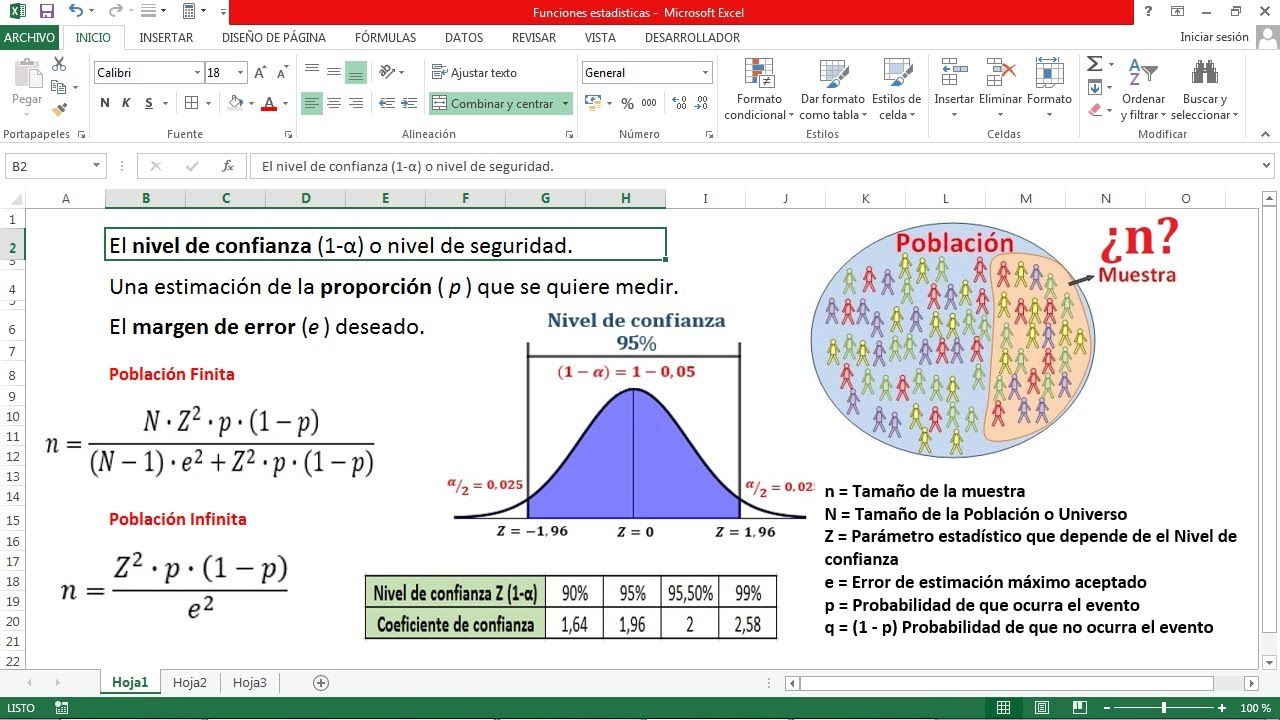
Cómo Calcular el Tamaño de la Muestra para Población Finita y Población Infinita con Excel.

Tamaño de Muestra para Variables Cuantitativas con Población Finita

Tamaño de la muestra (Formula de muestreo finita)

#2 Tamaño de la muestra | Estadística descriptiva

Como Calcular el tamaño de la Muestra.wmv

🔍👉 TAMAÑO DE MUESTRA / CÓMO CALCULAR el TAMAÑO DE MUESTRA PASO a PASO en EXCEL 👍
5.0 / 5 (0 votes)
