#2 Tamaño de la muestra | Estadística descriptiva
Summary
TLDREn este video de estadística descriptiva, se explica cómo determinar el tamaño adecuado de una muestra según el tipo de población (finita o infinita) y la naturaleza de la variable (cualitativa o cuantitativa). Se detallan conceptos clave como el nivel de confianza, el error de estimación, y las probabilidades de éxito (p) y fracaso (q), junto con el parámetro Z, que depende del nivel de confianza. A través de ejemplos, se demuestra cómo calcular el tamaño de la muestra, haciendo énfasis en cómo usar estas fórmulas para poblaciones finitas e infinitas, y variables cualitativas y cuantitativas.
Takeaways
- 📊 El tamaño de la muestra es clave en la estadística descriptiva para representar a una población de manera adecuada.
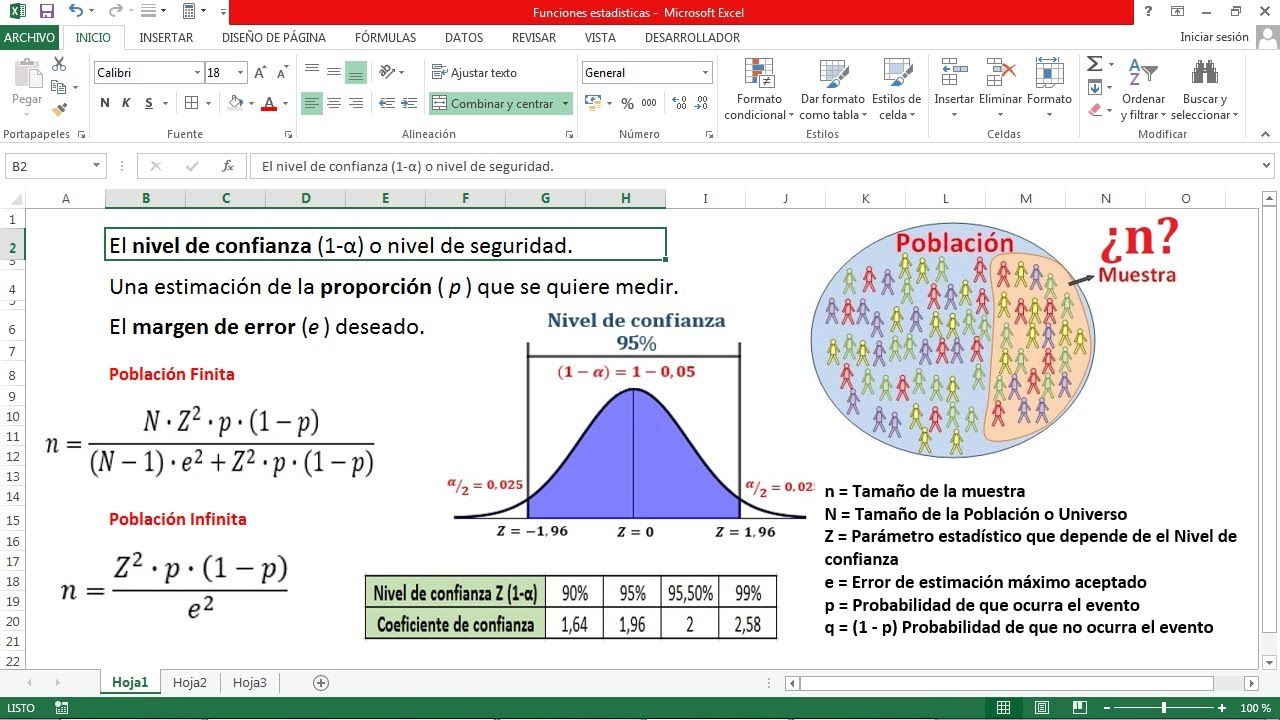
- 🧮 Existen dos tipos de poblaciones: finitas e infinitas. El método de cálculo del tamaño de la muestra varía según el tipo de población.
- 🎯 Para una variable cualitativa, el tamaño de la muestra se basa en la proporción y es fundamental diferenciar entre proporción y promedio.
- 🔍 El parámetro 'z' depende del nivel de confianza de la investigación, que suele variar entre el 90% y el 99%.
- ✔️ Un nivel de confianza del 95% es estándar y su valor asociado para 'z' es 1.96.
- ❓ La probabilidad de que algo ocurra se representa como 'p', mientras que 'q' representa la probabilidad de que no ocurra (q = 1 - p).
- 💡 El error de estimación (E) también depende del nivel de confianza, siendo común utilizar un margen de error del 5% (0.05).
- 📝 Para una población infinita, se utilizan fórmulas diferentes a las de una población finita, donde el tamaño de la población influye en el cálculo.
- 🔢 Cuando no se proporciona el valor de 'p' y 'q', se asume que ambos son 0.5.
- 📐 Para variables cuantitativas, en lugar de utilizar 'p' y 'q', se usa la varianza, que mide la dispersión de los datos.
Q & A
¿Qué es una muestra en términos de estadística descriptiva?
-Una muestra es un subconjunto de una población, y está formada por un grupo de individuos seleccionados de forma aleatoria para representar a toda la población en un análisis estadístico.
¿Por qué no es necesario estudiar a toda la población para realizar un análisis estadístico?
-No es necesario estudiar a toda la población porque con una muestra seleccionada adecuadamente se pueden obtener características representativas de la población, lo que facilita el análisis sin requerir el estudio completo de cada individuo.
¿Cuál es la diferencia entre una población finita e infinita?
-Una población finita es aquella donde se conoce el número total de elementos, mientras que una población infinita se considera cuando el número de elementos es tan grande que no puede ser contado de manera exacta.
¿Cómo afecta el tipo de variable (cualitativa o cuantitativa) al cálculo del tamaño de la muestra?
-El tipo de variable afecta la fórmula para calcular el tamaño de la muestra. Si la variable es cualitativa, se trabaja con proporciones. Si la variable es cuantitativa, se utiliza el promedio como indicador clave.
¿Qué es el nivel de confianza y cómo se utiliza en el cálculo del tamaño de la muestra?
-El nivel de confianza es la probabilidad de que los resultados de la muestra sean representativos de la población. En estadística, suele estar entre el 90% y el 99%. Un nivel de confianza estándar es el 95%, lo que implica un valor de 1.96 para el parámetro Z en los cálculos.
¿Qué representa el parámetro Z y cómo se relaciona con el nivel de confianza?
-El parámetro Z es un valor estadístico que depende del nivel de confianza seleccionado. Por ejemplo, un nivel de confianza del 95% corresponde a un valor de Z de 1.96, que se utiliza en la fórmula para calcular el tamaño de la muestra.
¿Qué es el error de estimación y cómo se calcula?
-El error de estimación es la diferencia aceptable entre el valor real de la población y el valor estimado a partir de la muestra. Se calcula restando el nivel de confianza al 100%, y se expresa como una fracción. Por ejemplo, con un nivel de confianza del 95%, el error de estimación sería 0.05.
¿Qué representan los valores de P y Q en el cálculo del tamaño de la muestra?
-El valor de P representa la probabilidad de que ocurra el evento que estamos estudiando, mientras que Q es la probabilidad de que no ocurra. Ambos se relacionan, ya que P + Q = 1. Estos valores son clave para determinar el tamaño de la muestra en variables cualitativas.
¿Qué se debe hacer si no se dispone de los valores de P y Q?
-Si no se dispone de los valores de P y Q, se asume un valor estándar del 50% para cada uno (P = 0.5 y Q = 0.5). Esto es una práctica común cuando no se tienen datos previos sobre las probabilidades de ocurrencia o no ocurrencia del evento.
¿Cómo cambia la fórmula para calcular el tamaño de la muestra en variables cuantitativas?
-En variables cuantitativas, en lugar de usar P y Q como en las cualitativas, se utiliza la varianza de la población, la cual se calcula o se obtiene a partir de datos anteriores. La varianza reemplaza a los valores de P y Q en la fórmula de la muestra.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Tamaño de Muestra para Variables Cualitativas con Población Finita
Cómo Calcular el Tamaño de la Muestra para Población Finita y Población Infinita con Excel.

Tamaño de Muestra para Variables Cuantitativas con Población Finita

How to determine the Sample Size?

Tamaño de Muestra para Variables Cuantitativas con Población Indefinida

Tamaño de la muestra (Formula de muestreo finita)
5.0 / 5 (0 votes)
