Cara menyusun fungsi kuadrat
Summary
TLDRIn this tutorial, the host explains how to form quadratic functions using various formulas, tailored to specific conditions like crossing the x-axis, touching the x-axis, passing through a maximum or minimum point, or going through three given points. The video walks through multiple examples with step-by-step solutions, demonstrating how to apply each formula effectively. Viewers learn to identify key values, substitute them into the respective equations, and solve for the unknowns, making the process of understanding and constructing quadratic functions simple and accessible.
Takeaways
- 😀 A brief introduction about a video discussing how to solve quadratic functions.
- 😀 The video encourages viewers to like, subscribe, comment, and share the video for potential benefits.
- 😀 The video outlines several formulas for constructing quadratic functions based on different conditions in problems.
- 😀 Formula 1: Used when a quadratic function intersects the x-axis and passes through a specific point. Formula is y = a(X - X1)(X - X2).
- 😀 Formula 2: Used when the quadratic function touches (is tangent to) the x-axis and passes through a specific point. Formula is y = a(X - X1)².
- 😀 Formula 3: Used when a quadratic function has a maximum or minimum point (vertex) and passes through another point. Formula is y = a(X - XP)² + YP.
- 😀 Formula 4: Used when a quadratic function passes through three specific points. Formula is y = ax² + bx + c.
- 😀 Step-by-step examples are provided to explain how to apply each formula to different problems.
- 😀 The importance of substituting values for x and y from the given points into the correct formula is highlighted.
- 😀 The video explains how to solve for the coefficient 'a' by substitution and solving equations, including how to handle negative signs and simplify expressions.
Q & A
What is the first formula used to construct a quadratic function when it cuts the x-axis and passes through a specific point?
-The first formula used is y = a * (X - X1) * (X - X2), where X1 and X2 are the x-intercepts, and the function passes through a specific point.
When the quadratic function touches the x-axis (tangent) and passes through a point, which formula should be used?
-The formula to use is y = a * (X - X1)^2, where X1 is the point of tangency on the x-axis, and the function passes through a specific point.
What is the formula for a quadratic function that passes through a vertex (maximum or minimum point) and another specific point?
-The formula for such a quadratic function is y = a * (X - XB)^2 + YP, where (XB, YP) is the vertex, and the function also passes through a specific point.
What formula is used when a quadratic function passes through three distinct points?
-The formula used for this case is y = ax^2 + bx + c, where a, b, and c are constants determined by substituting the three points into the equation.
In the first example, how do you determine the value of 'a' in the quadratic equation?
-To find 'a', substitute the known point (x = 0, y = -10) and the x-intercepts (X1 = -5 and X2 = 2) into the equation y = a * (X - X1) * (X - X2), then solve for 'a'.
Why does the formula y = a * (X - X1) * (X - X2) use the x-intercepts as X1 and X2?
-The x-intercepts, or roots of the quadratic equation, are the values where the curve intersects the x-axis. These are represented as X1 and X2 in the formula.
How do you solve for 'a' when using the formula y = a * (X - X1)^2 for a tangent quadratic function?
-Substitute the known point into the equation, solve for 'a' by simplifying the expression, and then compute 'a' by isolating it on one side of the equation.
What is the significance of the vertex in the formula y = a * (X - XB)^2 + YP?
-The vertex (XB, YP) represents the maximum or minimum point of the quadratic function, which is crucial in determining the function's shape and direction.
How do you solve for the coefficients a, b, and c in the equation y = ax^2 + bx + c when given three points?
-Substitute each of the three points (x, y) into the equation, creating a system of three equations. Then solve this system using substitution or elimination methods to find a, b, and c.
What method is used to solve the system of equations for finding a, b, and c in the fourth example?
-A combination of elimination and substitution is used to solve the system of equations. The method eliminates variables step by step to solve for each coefficient.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Fungsi Kuadrat Bagian 1 - Matematika Wajib Kelas X m4thlab
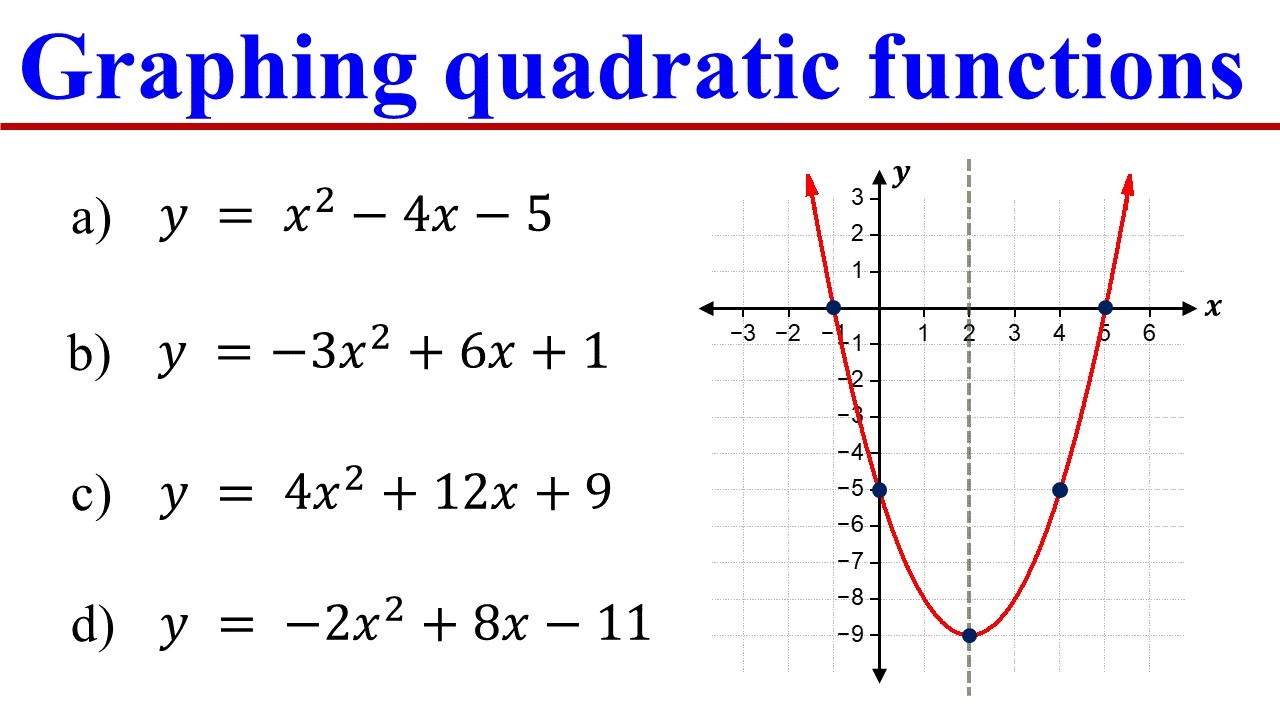
How to Graph Quadratic Functions by finding the Vertex, Axis of symmetry, X & Y intercepts

Menyusun Rumus Fungsi Kuadrat #fazanugas

Quadratic Functions, How to Graph Quadratic Functions, Quadratic Function Graph

Cara Menentukan Fungsi Kuadrat Jika Diketahui Titik Potong Terhadap Sumbu-X
FUNGSI KUADRAT
5.0 / 5 (0 votes)
