161. OCR A Level (H446) SLR26 - 2.3 Comparison of the complexity of algorithms
Summary
TLDRThis video delves into Big O notation, explaining the time and space complexity of various algorithms. It covers common data structures like arrays, lists, stacks, queues, hash tables, linked lists, and binary trees, analyzing operations such as insertion, deletion, searching, and sorting. The video emphasizes the importance of worst-case time complexity while also touching on best and average cases. It also introduces the concept of space complexity and discusses the efficiency of sorting algorithms like bubble sort, insertion sort, merge sort, and quicksort. A helpful summary of key algorithms is provided for exam preparation.
Takeaways
- 😀 Big O notation is essential for comparing the efficiency of algorithms in terms of time complexity.
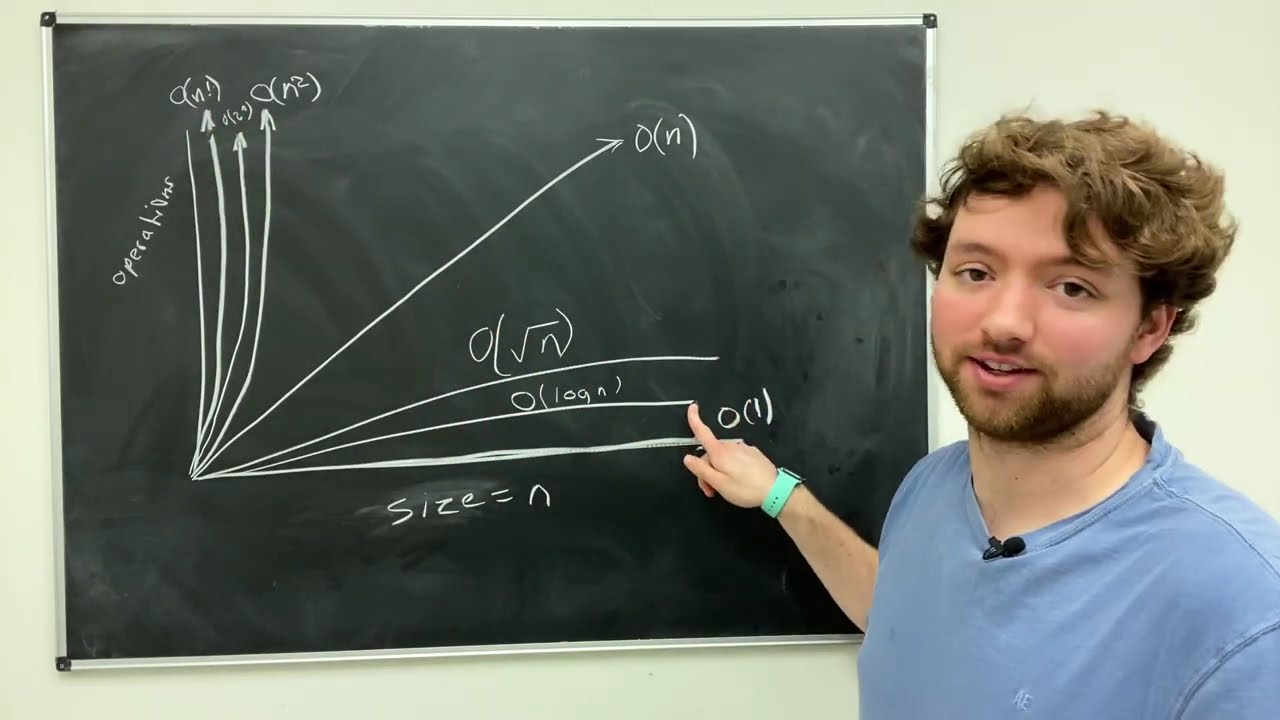
- 😀 Linear search in an unsorted array has a time complexity of O(n), but in the best case, it can be O(1).
- 😀 A sorted array allows the use of binary search, which has a time complexity of O(log n) for searching.
- 😀 Adding items to an array or list typically has a constant time complexity of O(1), regardless of the size of the array.
- 😀 When inserting into or deleting from a linked list, the time complexity is O(1) since no shifting of elements is required.
- 😀 Hash tables offer O(1) constant time complexity for searching, inserting, and deleting, but may require overflow handling in case of hash collisions.
- 😀 Stacks and queues have O(1) time complexity for their basic operations (push/pop for stacks, enqueue/dequeue for queues).
- 😀 Binary trees have a logarithmic time complexity of O(log n) for insertion and searching, but linear O(n) time complexity for complete traversal.
- 😀 Sorting algorithms like bubble sort and insertion sort have a polynomial time complexity of O(n^2) due to their nested loops.
- 😀 When comparing algorithms, both time and space complexity should be considered. Some algorithms, like merge sort, require O(n) space, while quicksort requires O(log n).
- 😀 Big O notation describes worst-case scenarios, while best and average cases are represented by Big Omega and Big Theta respectively.
Q & A
What is the main focus of this video?
-The video focuses on comparing the complexity of various algorithms using Big O notation, assuming the viewer has prior knowledge of basic data structures and algorithms.
What is Big O notation and why is it important in algorithm analysis?
-Big O notation is a way of expressing the time complexity of an algorithm, particularly in terms of its worst-case performance as the size of the input grows. It helps compare the efficiency of different algorithms.
What is the time complexity of adding an item to an array or list?
-Adding an item to an array or list, where the item is placed at the end, has a constant time complexity of O(1), regardless of the array's size.
How does the time complexity of a linear search compare to binary search?
-A linear search has a time complexity of O(n), meaning the time to search increases linearly with the size of the data set. In contrast, a binary search, applied to sorted data, has a time complexity of O(log n), meaning the search time grows logarithmically as the dataset size increases.
What is the advantage of using a sorted array for searching?
-The advantage of using a sorted array for searching is that it allows the use of a binary search, which is much more efficient than a linear search, reducing the time complexity to O(log n).
What is the time complexity of inserting an item into a sorted array?
-Inserting an item into a sorted array requires shifting elements to maintain order, which results in a time complexity of O(n), as the number of shifts increases with the array size.
What is the time complexity of stack and queue operations?
-Stack and queue operations such as push, pop, enqueue, and dequeue have constant time complexity, O(1), as the size of the stack or queue does not affect these operations.
How does hashing improve the efficiency of lookups?
-Hashing improves lookup efficiency by using a hashing algorithm to directly compute the index of an item, making the time complexity O(1). However, in cases of hash collisions (synonyms), an overflow table may need to be searched, leading to a time complexity of O(n) for those specific cases.
What is the time complexity of searching a linked list?
-Searching a linked list has a linear time complexity of O(n) because, like arrays, each item must be checked one by one until the target is found.
What is the time complexity for inserting or deleting items in a linked list?
-Inserting or deleting items in a linked list has a constant time complexity of O(1) because no elements need to be shifted; the operation only involves updating pointers.
What are the time complexities of bubble sort and insertion sort?
-Both bubble sort and insertion sort have a time complexity of O(n^2) due to their nested loops. These algorithms are considered quadratic in nature.
What is the difference between best, average, and worst case scenarios in algorithm analysis?
-The best case represents the optimal scenario where the algorithm performs the least amount of work, the average case reflects typical performance, and the worst case represents the maximum amount of work the algorithm may require. Big O notation typically describes the worst-case scenario.
What is space complexity, and how does it relate to time complexity?
-Space complexity refers to the amount of memory an algorithm requires during execution, while time complexity measures how the running time increases with input size. Some algorithms, like merge sort, have higher space complexity (O(n)) compared to others like quicksort (O(log n)) due to their memory usage.
What is the significance of considering both time and space complexity when choosing algorithms?
-Considering both time and space complexity is crucial because an algorithm may be fast in terms of execution time but consume excessive memory, or it may use minimal memory but be slow. A balance between both factors is often necessary for efficient algorithm design.
What does the term 'big theta' refer to, and how does it differ from Big O notation?
-Big Theta (Θ) describes the average case time complexity of an algorithm, whereas Big O notation focuses on the worst-case scenario. Big O is used more widely in analysis, especially when comparing the efficiency of algorithms.
Why are best and average case scenarios not always considered when analyzing algorithms in Big O notation?
-Big O notation focuses on the worst-case scenario to provide a guaranteed upper bound on performance, which ensures that the algorithm will not perform worse than a certain threshold, regardless of input. This simplification helps in comparing algorithms across different scenarios.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Introduction to Big-O

Time & Space Complexity - Big O Notation - DSA Course in Python Lecture 1

HOW TO COMPUTE TIME COMPLEXITY AND SPACE COMPLEXITY OF AN ALGORITHM

Big O Notation: O Pesadelo do Programador Iniciante
Time Complexity and Big O Notation - Data Structures and Algorithms

L-1.3: Asymptotic Notations | Big O | Big Omega | Theta Notations | Most Imp Topic Of Algorithm
5.0 / 5 (0 votes)
