LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 3
Summary
TLDRThe video explores fundamental concepts in fluid dynamics, focusing on the conservation of mass and momentum. It explains how the continuity equation can be simplified for two-dimensional flow, introducing the stream function to represent flow lines. The discussion then delves into the Navier-Stokes equations, showing how the momentum conservation equation is derived and how shear stress is related to the velocity field. The video concludes with the application of these equations to solve real-world fluid flow problems, emphasizing the need for constitutive equations and boundary conditions in mathematical solutions.
Takeaways
- 😀 The continuity equation for two-dimensional flow can be simplified into a stream function, representing flow lines in a fluid field.
- 😀 Fluid flow problems require both the continuity equation and momentum conservation equations to be solved, which are integral in understanding the behavior of the fluid.
- 😀 The conservation of momentum equation can be transformed from integral form to differential form using divergence theorem, leading to the Cauchy equation.
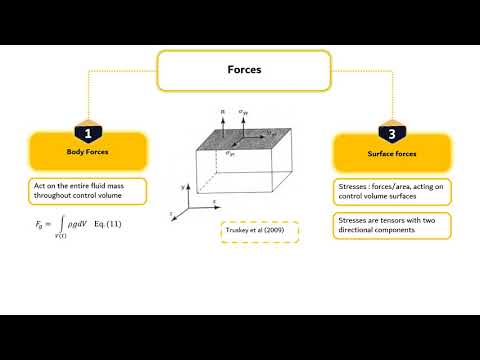
- 😀 The Cauchy equation can be rewritten using the chain rule in calculus, but its usefulness is limited due to the complex stress tensor with multiple independent components.
- 😀 The solution of fluid flow equations requires additional equations known as constitutive equations, which help express stress tensor components in terms of velocity and pressure fields.
- 😀 The process of separating normal stress (pressure) and shear stress (viscosity) in fluid flow helps reduce the complexity of the stress tensor.
- 😀 Shear stress in a fluid is proportional to the shear strain rate, especially in Newtonian fluids, which simplifies the stress-strain relationship.
- 😀 Substituting the shear stress-strain relationship into the Cauchy stress tensor leads to a new set of equations that combine with the continuity equation to form the Navier-Stokes equations.
- 😀 The Navier-Stokes equations consist of one continuity equation and three momentum equations, with four unknown variables: three velocity components and one pressure component.
- 😀 The Navier-Stokes equations can be solved mathematically for fluid flow problems, including calculating pressure for a known velocity field or determining velocity and pressure for specific geometries and boundary conditions.
Q & A
What is the continuity equation in fluid dynamics?
-The continuity equation expresses the conservation of mass in a fluid flow. In two-dimensional flow, it can be simplified into a form involving a stream function, which represents the flow lines in the fluid field.
What is a stream function and how is it used in fluid dynamics?
-A stream function is a mathematical representation of flow lines in a fluid field. It is used to simplify the continuity equation and can represent the lines of constant flow in the system.
What additional equation is needed for solving fluid flow problems apart from the continuity equation?
-Apart from the continuity equation, the conservation of momentum equation, known as the Navier-Stokes equation, is needed to solve fluid flow problems.
What is the importance of constitutive equations in fluid dynamics?
-Constitutive equations are crucial because they allow the components of the stress tensor to be expressed in terms of the velocity and pressure fields, which reduces the number of unknown variables and makes the system solvable.
How is the stress tensor decomposed in fluid dynamics?
-The stress tensor is decomposed into normal stress (pressure), which acts perpendicular to the surface, and shear stress (viscosity), which represents the internal friction between fluid layers.
What is the relationship between shear stress and shear strain rate for Newtonian fluids?
-For Newtonian fluids, the shear stress is directly proportional to the shear strain rate. This linear relationship simplifies the stress tensor and is fundamental for deriving the Navier-Stokes equations.
How do the Navier-Stokes equations incorporate the stress tensor?
-The Navier-Stokes equations incorporate the stress tensor by substituting the relationship between shear stress and strain rate, which simplifies the equations and allows for the modeling of fluid flow under various conditions.
What is the significance of the Navier-Stokes equations in fluid dynamics?
-The Navier-Stokes equations are fundamental in fluid dynamics as they describe the motion of fluid substances, including the interaction of velocity, pressure, and viscosity within the fluid field.
How are the Navier-Stokes equations solved for fluid flow problems?
-The Navier-Stokes equations are solved by applying boundary and initial conditions along with known velocity fields or geometries. The equations can be solved numerically or analytically depending on the complexity of the flow.
What coordinate systems are used for solving fluid flow problems using the Navier-Stokes equations?
-The Navier-Stokes equations can be applied in different coordinate systems, such as Cartesian and cylindrical coordinates, depending on the geometry and nature of the fluid flow problem.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
5.0 / 5 (0 votes)