Lesson 4 - Moving Control Volumes

Summary

In this lecture, the focus is on the Reynolds Transport Theorem, conservation of mass, and conservation of momentum, particularly in the context of moving control volumes. The theorem is explained in terms of system changes and the flow across control volume boundaries. For steady-state conditions, the conservation of mass and momentum are derived in a way that simplifies to relative velocities. The session also discusses a practical problem involving an inclined ramp moving with a jet, demonstrating how these concepts apply to real-world fluid mechanics scenarios, such as determining the force exerted on water due to the ramp's motion.

Takeaways

• 😀 The Reynolds transport theorem connects the system and control volume perspectives in fluid mechanics.
• 😀 Conservation of mass and momentum are fundamental concepts discussed in relation to control volume movement.
• 😀 A moving control volume is analyzed in an inertial reference frame (non-accelerating frame).
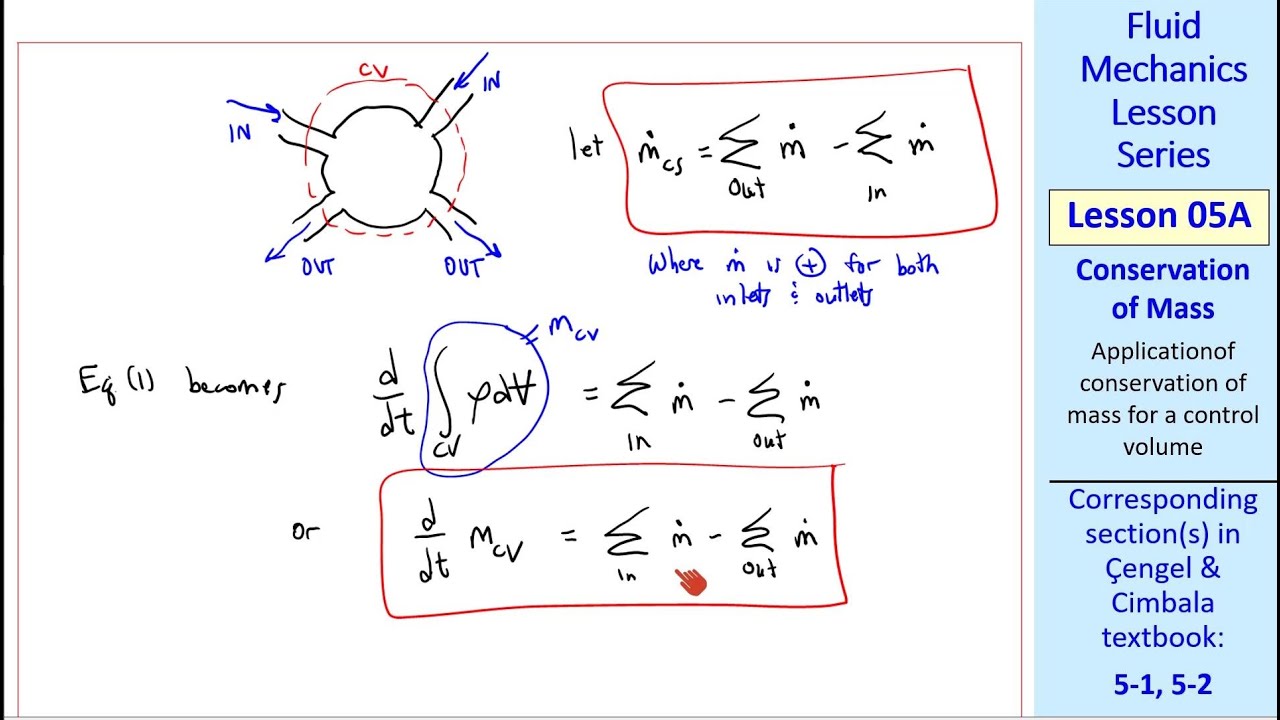
• 😀 The mass flow across the boundary depends on the relative velocity (W) between the control volume and the fluid.
• 😀 The absolute velocity of the fluid is a combination of the control volume velocity (V_CV) and the relative velocity (W).
• 😀 For steady-state problems, the rate of change of mass and momentum becomes zero, simplifying the equations.
• 😀 Conservation of momentum is derived using relative velocity, focusing on steady-state problems in an inertial control volume.
• 😀 The mass flow rate across the control surface is expressed in terms of relative velocity, simplifying calculations.
• 😀 In steady-state conservation of momentum, forces acting on the control volume are related to the momentum flux through the control surface.
• 😀 If flow enters and exits a system at the same velocity, there is no net force in the direction of flow, implying no momentum generation in that direction.
• 😀 The upcoming class problem involves calculating the force on water as it flows over an inclined plane moving at a constant velocity.

Q & A

What is the Reynolds transport theorem?

The Reynolds transport theorem relates the system perspective (Lagrangian) to the control volume perspective (Eulerian) in fluid mechanics. It accounts for changes within a moving system and the mass or momentum crossing the control volume boundary.

What does the term 'control volume' refer to in fluid mechanics?

A control volume is a fixed region of interest in space through which fluid flows, used for analyzing the mass, momentum, and energy balance in fluid systems.

How does the motion of a control volume affect the conservation of mass equation?

When the control volume is moving, the conservation of mass equation is modified to account for relative velocity across the boundary of the control volume. The mass flow across the boundary is due to the relative velocity, not the absolute velocity.

What is the significance of the term 'v.n' in the Reynolds transport theorem?

'v.n' represents the flow of mass across the boundary of the control volume relative to the boundary. It indicates the rate at which mass enters or exits the control volume.

How is the absolute velocity of the fluid related to the velocity of the control volume?

The absolute velocity of the fluid is the sum of the control volume's velocity and the relative velocity of the fluid within the control volume. This combined velocity is observed from a stationary reference frame.

What happens when the control volume is moving with respect to the fluid?

When the control volume is moving, the velocity of the fluid relative to the control volume becomes the key factor in determining mass and momentum flow across the boundary. The absolute velocity is the sum of the control volume velocity and the relative velocity.

What is the importance of steady-state analysis in conservation of momentum?

In steady-state analysis, the time derivative terms are zero, simplifying the conservation of momentum equation. This allows for easier analysis by eliminating the need to consider transient changes within the control volume.

What does the equation for conservation of momentum look like for a moving control volume?

The conservation of momentum equation for a moving control volume, under steady-state conditions, simplifies to an expression involving the relative velocity of the fluid with respect to the control volume, excluding time-dependent terms.

Why is it necessary to consider the relative velocity of the fluid in moving control volumes?

The relative velocity is essential because it accurately reflects how the fluid behaves within the moving control volume. It allows for a more accurate description of mass and momentum flux across the control surface.

What happens if the velocity of the fluid entering and exiting a control volume is the same?

If the fluid enters and exits the control volume with the same velocity, there is no net force in that direction. This means that no momentum is transferred across the boundary, resulting in zero net force from the flow.