Find center and radius of circumference (completing perfect square trinomial)
Summary
TLDREn este video, se explica cómo encontrar el centro y el radio de una circunferencia a partir de su ecuación general. El proceso incluye completar el trinomio cuadrado perfecto para reescribir la ecuación en su forma ordinaria. Se detallan los pasos para dividir los coeficientes, elevar al cuadrado y simplificar. Finalmente, se obtiene el centro de la circunferencia a partir de los coeficientes de la ecuación y el radio al calcular la raíz cuadrada de un valor resultante. El video concluye con una invitación a dejar comentarios y sugerencias, y suscribirse al canal.
Takeaways
- 😀 El video enseña cómo encontrar el centro y el radio de una circunferencia a partir de su ecuación general.
- 😀 Se utiliza el proceso de completar el trinomio cuadrado perfecto para transformar la ecuación.
- 😀 Primero se escribe el término cuadrado de x y el término lineal en x (8x) para completar el trinomio.
- 😀 Se divide el coeficiente de x entre dos y luego se eleva al cuadrado para agregarlo a la ecuación.
- 😀 Lo mismo se hace con el término cuadrado de y y el término lineal en y (-4y).
- 😀 Después de agregar los términos necesarios, se reacomoda la ecuación y se iguala al otro lado.
- 😀 Los términos agregados deben ser balanceados en ambos lados de la ecuación para mantener la igualdad.
- 😀 La ecuación se simplifica a un binomio al cuadrado para x y otro para y, lo que facilita encontrar el centro y el radio.
- 😀 Para encontrar el centro, se toma el valor opuesto de los números dentro de los binomios: -4 y 2.
- 😀 El radio se obtiene sacando la raíz cuadrada del número constante que queda a la derecha de la ecuación, que en este caso es 16, y su raíz cuadrada es 4.
- 😀 El centro de la circunferencia es (-4, 2) y su radio es 4, como se obtiene de la ecuación final.
- 😀 Se invita a los espectadores a dejar comentarios, dudas, sugerencias, o ejercicios que les gustaría ver en futuros videos.
Q & A
¿Qué es lo que se busca encontrar en el video?
-En el video se busca encontrar el centro y el radio de una circunferencia a partir de su ecuación general.
¿Qué es un trinomio cuadrado perfecto?
-Un trinomio cuadrado perfecto es una expresión algebraica de la forma (x + a)^2 o (x - a)^2, que al expandirla da un trinomio con términos específicos, como x^2, 2ax y a^2.
¿Qué pasos se siguen para completar el trinomio cuadrado perfecto?
-Primero se toman los términos x^2 y 8x. Luego, se divide el coeficiente de x entre 2 y se eleva al cuadrado. Se repite el proceso con el término y. Finalmente, se añaden estos términos para completar el cuadrado.
¿Cómo se maneja el término independiente al completar el trinomio cuadrado perfecto?
-El término independiente se maneja trasladando los términos adicionales al otro lado de la ecuación para mantener la igualdad, ya que no se pueden agregar términos sin agregar los mismos en ambos lados de la ecuación.
¿Cómo se determina el centro de la circunferencia?
-El centro se determina a partir de las coordenadas del binomio cuadrado resultante, cambiando el signo del valor de x y y. Si el binomio tiene la forma (x + h)^2 y (y - k)^2, el centro será (-h, k).
¿Qué fórmula se usa para calcular el radio de la circunferencia?
-El radio se calcula sacando la raíz cuadrada del número que aparece a la derecha de la ecuación. Si el número es 16, el radio será la raíz cuadrada de 16, que es 4.
¿Qué sucede si no se suman o restan los términos correctamente en ambos lados de la ecuación?
-Si no se suman o restan los términos correctamente en ambos lados, la ecuación no estará equilibrada y el proceso de encontrar el centro y el radio no dará resultados correctos.
¿Por qué se usa el proceso de completar el trinomio cuadrado perfecto en la ecuación?
-Se utiliza para reescribir la ecuación de la circunferencia en su forma estándar, que permite identificar fácilmente el centro y el radio de la circunferencia.
¿Qué significa que la ecuación se convierta en una forma ordinaria?
-Que la ecuación de la circunferencia se haya transformado en una forma reconocida, como (x - h)^2 + (y - k)^2 = r^2, donde (h, k) son las coordenadas del centro y r es el radio.
¿Cómo se encuentran las coordenadas del centro?
-Las coordenadas del centro se encuentran tomando los valores de los binomios en la forma (x - h)^2 y (y - k)^2 y cambiando los signos: si el signo es positivo, se toma negativo, y si es negativo, se toma positivo.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Circunferencias: De general a ordinaria | Matemáticas | Khan Academy en Español

Ecuación de la circunferencia con centro fuera del origen (tercera parte).

Encontrar el centro y radio de la CIRCUNFERENCIA conociendo la ecuación general EJEMPLO 2

Hallar la ecuación general de la CIRCUNFERENCIA conociendo el centro y el radio EJEMPLO 2
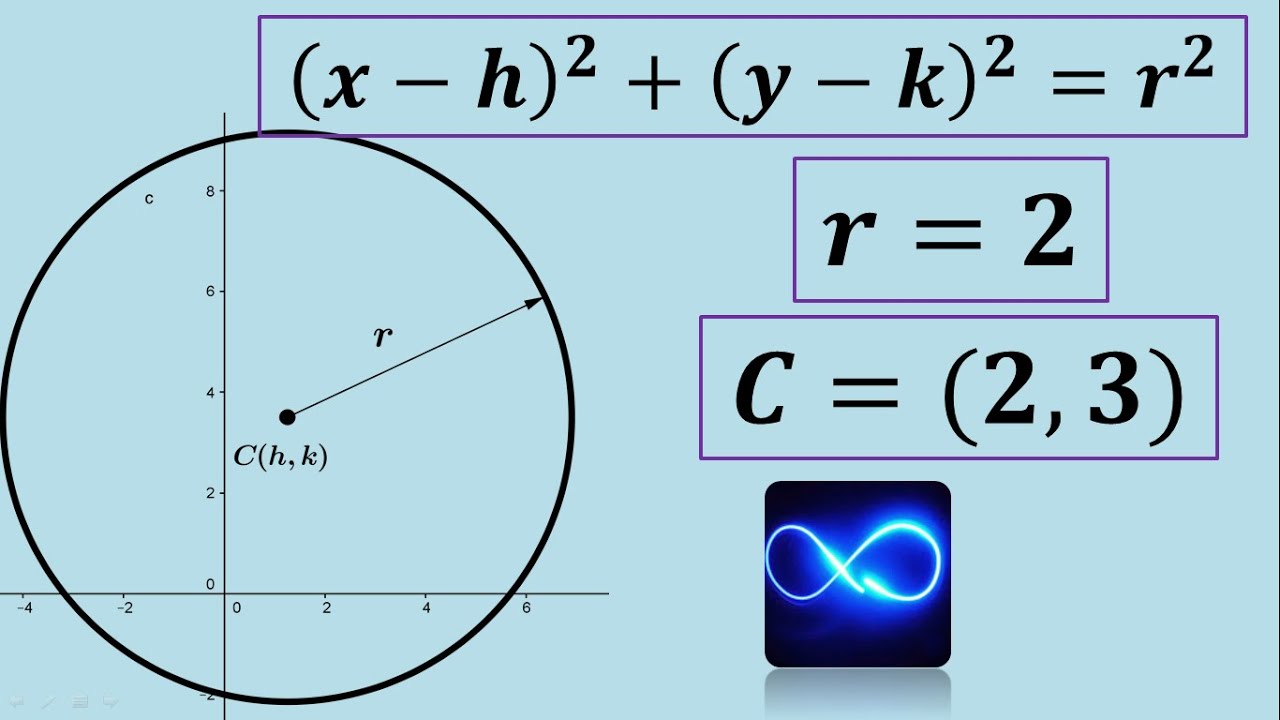
Ordinary and general equation of circumference with given center and radius (Example 1)

32. Ecuación de la circunferencia con centro fuera del origen
5.0 / 5 (0 votes)
