Ecuación canónica o simétrica de la recta
Summary
TLDREn este video, se explica de manera clara la ecuación canónica o simétrica de la recta, abordando conceptos fundamentales como la abscisa y la ordenada en el origen. A través de ejemplos prácticos, se muestra cómo graficar rectas usando esta ecuación, ubicando los puntos de corte con los ejes X y Y. Además, se detallan situaciones con signos negativos en la ecuación, y cómo afectan al gráfico. El video invita a los estudiantes a explorar más sobre el tema en un curso completo disponible en el canal, y a interactuar con el contenido mediante comentarios y suscripciones.
Takeaways
- 😀 La ecuación canónica o simétrica de la recta tiene la forma: x/a + y/b = 1.
- 😀 La 'a' representa la abscisa en el origen, es decir, el punto de corte con el eje x.
- 😀 La 'b' representa la ordenada en el origen, es decir, el punto de corte con el eje y.
- 😀 Un beneficio de la ecuación canónica es que es fácil de graficar identificando directamente los puntos de corte con los ejes.
- 😀 En la ecuación x/3 + y/5 = 1, el punto de corte con el eje x es 3 y el punto de corte con el eje y es 5.
- 😀 Para graficar, solo se necesitan los puntos de corte con los ejes x y y, y luego trazar la recta.
- 😀 Si la ecuación contiene valores negativos, estos indican que los puntos de corte están en el lado opuesto de los ejes.
- 😀 En el caso de la ecuación x/3 - y/4 = 1, la abscisa sigue siendo 3, pero la ordenada es -4, lo que indica un corte debajo del eje y.
- 😀 La ecuación puede ser reescrita para facilitar su interpretación, por ejemplo, transformando el signo negativo en el denominador.
- 😀 La visualización de los puntos de corte es clave para graficar correctamente la recta en un plano cartesiano.
- 😀 Se recomienda practicar con diferentes valores de los coeficientes para comprender bien cómo afectan la posición de la recta en el plano.
Q & A
¿Qué es la ecuación canónica o simétrica de la recta?
-Es una forma de representar la ecuación de la recta en la que se utilizan las abscisas y ordenadas en el origen para definir el punto de corte de la recta con los ejes X y Y respectivamente.
¿Qué representa la 'a' en la ecuación canónica de la recta?
-La 'a' representa la abscisa en el origen, es decir, el punto donde la recta corta el eje X.
¿Qué significa la 'b' en la ecuación canónica de la recta?
-La 'b' representa la ordenada en el origen, es decir, el punto donde la recta corta el eje Y.
¿Cómo se puede graficar una recta usando la ecuación canónica?
-Para graficar una recta con la ecuación canónica, se deben ubicar los puntos de corte con el eje X y el eje Y, luego conectar estos puntos para formar la recta.
¿Qué sucede si los valores de los puntos de corte son negativos?
-Si los valores son negativos, los puntos de corte con los ejes X o Y se ubican en la dirección opuesta, es decir, hacia la izquierda en el eje X o hacia abajo en el eje Y.
¿Cuál es el beneficio de usar la ecuación canónica para graficar?
-El beneficio principal es que es una de las ecuaciones más fáciles de graficar, ya que solo se necesita identificar los puntos de corte con los ejes X y Y.
¿Qué representa el signo negativo en la ecuación canónica?
-El signo negativo indica que uno de los puntos de corte está en una posición opuesta al origen, por ejemplo, un punto de corte negativo en el eje Y estaría por debajo del eje X.
¿Cómo se modificaría la ecuación si el valor de uno de los puntos de corte es negativo?
-Si uno de los valores es negativo, simplemente se refleja la posición del punto de corte sobre el eje correspondiente, ya sea X o Y, sin cambiar el resto de la ecuación.
¿Qué significa que la ecuación esté escrita de la forma 'x sobre 3 + y sobre 5 = 1'?
-Esta forma significa que la recta corta el eje X en el punto 3 y el eje Y en el punto 5. Al graficar, se ubicará un punto en el eje X en 3 y un punto en el eje Y en 5.
¿Cómo se podría graficar la ecuación 'x sobre 3 - y sobre 4 = 1'?
-Para graficar esta ecuación, primero se identificaría el punto de corte en el eje X (3) y el punto de corte en el eje Y (-4), ubicando estos puntos en el plano cartesiano y trazando la recta que los conecta.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Ecuaciones de la recta y sus transformaciones

Tipos de rectas: Horizontal, vertical e inclinada

Ex 6: Conic Section: Parabola with Horizontal Axis and Vertex NOT at the Origin (Right)
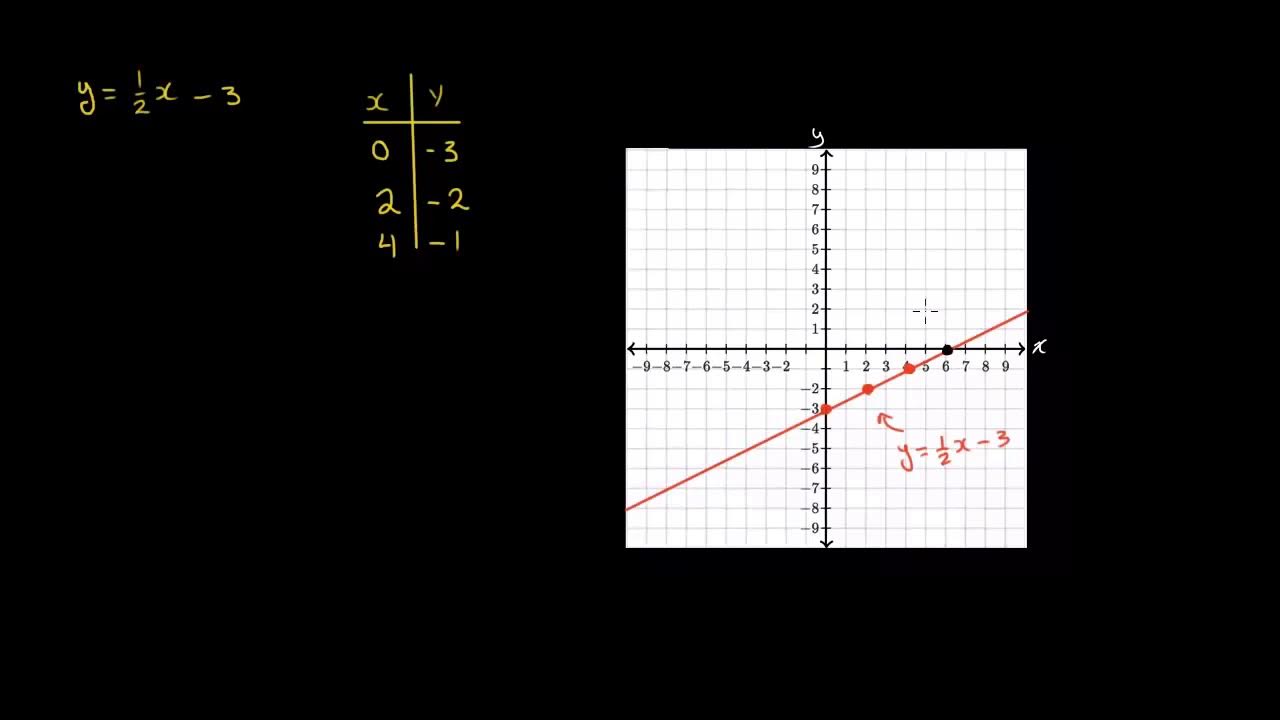
Introducción a las intersecciones con los ejes

HALLAR LA EXCENTRICIDAD Y LA ECUACIÓN DE UNA ELIPSE
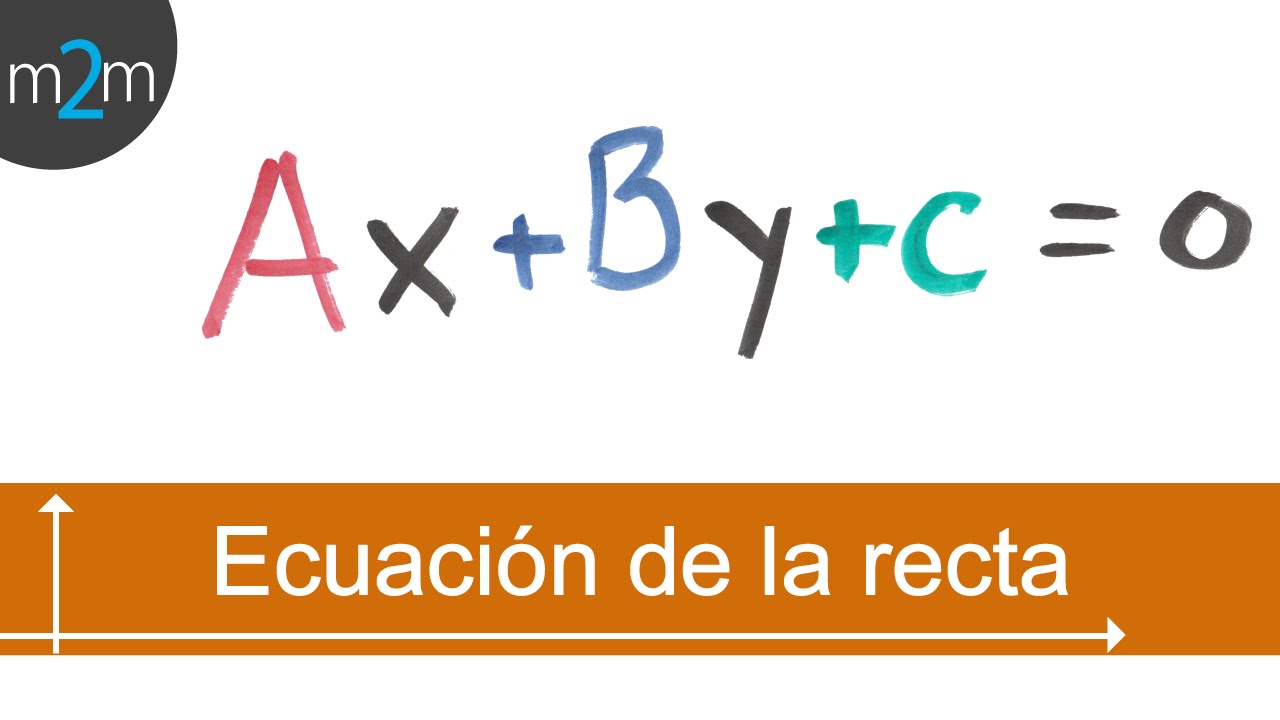
Ecuación general de la recta
5.0 / 5 (0 votes)
