HALLAR LA EXCENTRICIDAD Y LA ECUACIÓN DE UNA ELIPSE
Summary
Please replace the link and try again.
Please replace the link and try again.
Q & A
What is the eccentricity of an ellipse and how is it calculated?
-The eccentricity of an ellipse is a measure of how elongated the ellipse is. It is calculated using the formula: e = √(1 - b²/a²), where 'a' is the semi-major axis, and 'b' is the semi-minor axis.
How can we determine the equation of an ellipse given its center at the origin?
-The equation of an ellipse with its center at the origin and a vertical major axis is given by: (x²/b²) + (y²/a²) = 1, where 'a' is the semi-major axis and 'b' is the semi-minor axis.
What does it mean when the center of an ellipse is at the origin and one of its vertices is at (0, -7)?
-This means the semi-major axis of the ellipse is vertical, with one of the vertices at (0, -7). The distance from the center to the vertex (which is 7) gives the value of 'a' for the ellipse.
How do you calculate the value of 'a' from the given vertex of the ellipse?
-The value of 'a' is the distance from the center of the ellipse to one of its vertices. In this case, the vertex is at (0, -7), so 'a' is 7.
What equation do we use to find the semi-minor axis 'b' of the ellipse?
-To find the semi-minor axis 'b', we substitute a known point that lies on the ellipse into the canonical form of the equation and solve for 'b'.
How do you substitute a given point into the equation of an ellipse?
-To substitute a point into the equation, you replace the x and y coordinates of the point in place of x and y in the equation, then solve for the unknown variable (in this case, 'b').
What is the equation of the ellipse once you know the values of 'a' and 'b'?
-Once 'a' and 'b' are known, the equation of the ellipse is: (x²/b²) + (y²/a²) = 1. For this case, the equation is (x²/9) + (y²/49) = 1.
How do you calculate the eccentricity after finding 'a' and 'b'?
-After finding 'a' and 'b', the eccentricity can be calculated using the formula: e = √(1 - b²/a²). For this case, the eccentricity is √(1 - 9/49), which simplifies to 2√10/7.
Why is the eccentricity important in understanding the shape of an ellipse?
-The eccentricity indicates how much an ellipse deviates from being a circle. A value of 0 corresponds to a circle, and the closer the value is to 1, the more elongated the ellipse is.
What does the value of 'b' represent in the context of an ellipse?
-The value of 'b' represents the length of the semi-minor axis of the ellipse, which is the shortest distance from the center to the edge of the ellipse along its minor axis.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Geometría Analítica: Ecuación de la elipse dados foco y la excentricidad.

63. Encontrar a todos los elementos de una elipse cuando te dan su ecuación general.
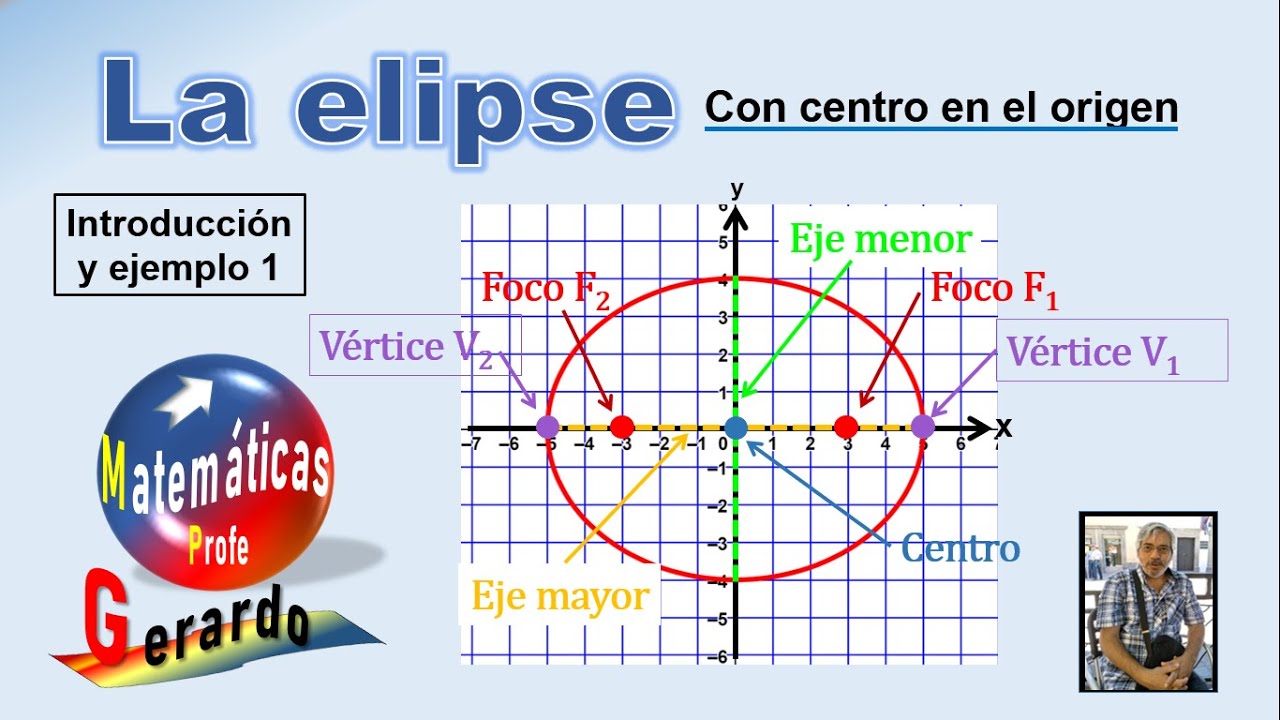
La elipse con centro en el origen. Introducción y ejemplo 1.

Ecuación canónica de la Elipse | Centro (0,0)

✅ELIPSE con centro FUERA del ORIGEN [100% 𝙀𝙛𝙚𝙘𝙩𝙞𝙫𝙤 😎🫵💯] Geometría Analítica
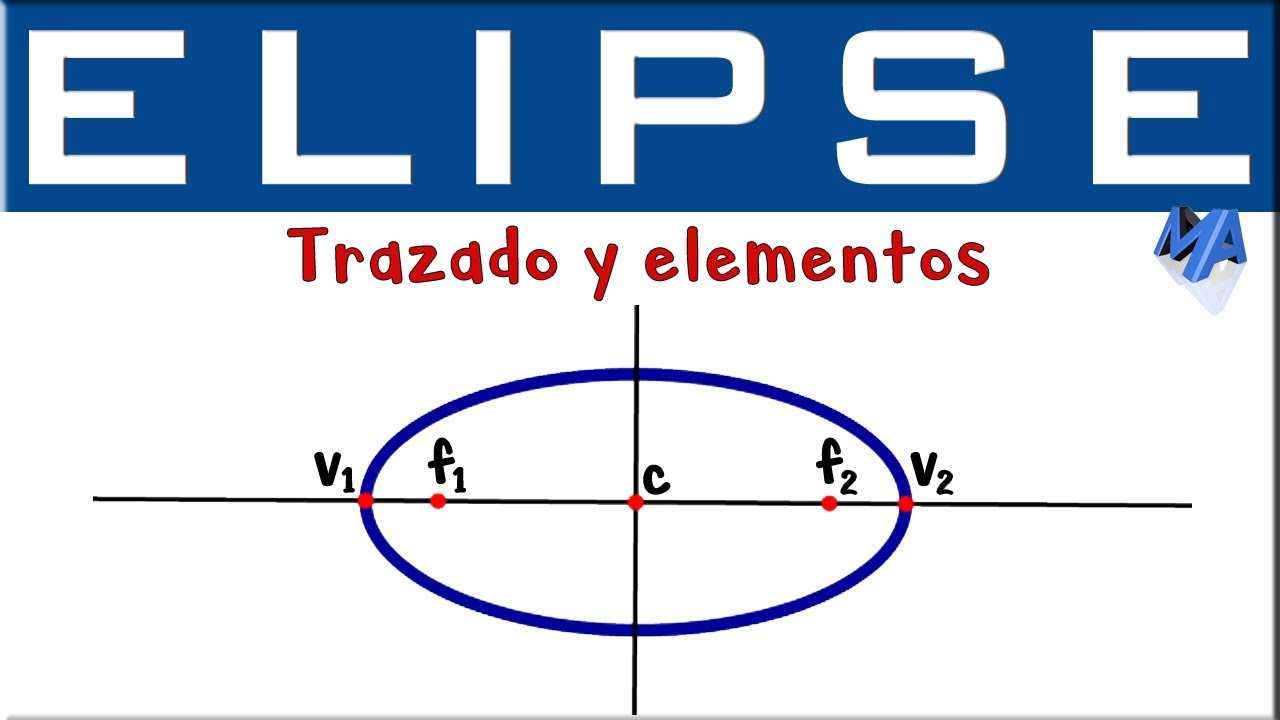
Elipse trazado y elementos | Introducción
5.0 / 5 (0 votes)