Distancia entre dos puntos ejemplo 3 método gráfico
Summary
TLDREn este video, se explica cómo calcular la distancia entre dos puntos en un plano cartesiano utilizando el teorema de Pitágoras. Se toman como ejemplo los puntos A (-3,6) y B (1,3), que se ubican en el gráfico, y se dibuja un triángulo rectángulo. La distancia entre los puntos es la hipotenusa del triángulo, que se calcula sumando los cuadrados de los catetos y luego aplicando la raíz cuadrada. El resultado es que la distancia es 5 unidades. El instructor invita a los espectadores a seguir el curso completo y participar en la comunidad con comentarios y likes.
Takeaways
- 📏 El tema principal del video es cómo hallar la distancia entre dos puntos en un plano cartesiano.
- 📝 Se utiliza un gráfico para explicar el proceso, con los puntos A (-3, 6) y B (1, 3).
- 📊 Los puntos A y B son ubicados en el plano cartesiano en las coordenadas correspondientes.
- 📐 Para hallar la distancia, se dibuja un triángulo rectángulo donde la hipotenusa es la distancia entre los dos puntos.
- 🔺 Los catetos del triángulo tienen longitudes de 3 unidades y 4 unidades, respectivamente.
- 📚 Se aplica el teorema de Pitágoras para encontrar la hipotenusa, usando la fórmula: hipotenusa² = cateto₁² + cateto₂².
- 🔢 Los valores de los catetos son elevados al cuadrado (3² = 9 y 4² = 16), sumándose para obtener 25.
- ✔️ La hipotenusa es la raíz cuadrada de 25, lo que da un resultado de 5.
- ✏️ La distancia entre los puntos A y B es 5 unidades.
- 👋 Al final del video, se invita a los espectadores a ver el curso completo y a interactuar con el contenido (dar like, comentar, compartir).
Q & A
¿Qué puntos se utilizan en el ejemplo para calcular la distancia?
-Los puntos utilizados son A (-3, 6) y B (1, 3).
¿Cómo se determinan las coordenadas de los puntos en el plano cartesiano?
-Se ubican las coordenadas de acuerdo a los ejes x e y, donde A está en (-3, 6) y B en (1, 3), y se marcan en el plano.
¿Qué método se utiliza para calcular la distancia entre dos puntos?
-Se utiliza el teorema de Pitágoras, creando un triángulo rectángulo donde la hipotenusa es la distancia que se quiere calcular.
¿Cuáles son los catetos del triángulo rectángulo en este caso?
-Un cateto mide 3 unidades y el otro cateto mide 4 unidades.
¿Qué establece el teorema de Pitágoras?
-El teorema de Pitágoras establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
¿Cómo se calcula la hipotenusa en este caso?
-Se suman los cuadrados de los catetos (3^2 = 9 y 4^2 = 16) para obtener 25, luego se saca la raíz cuadrada de 25, que es 5.
¿Qué representa la hipotenusa en este contexto?
-La hipotenusa representa la distancia entre los puntos A y B.
¿Por qué se aplica la raíz cuadrada al final del cálculo?
-Se aplica la raíz cuadrada para eliminar el exponente al cuadrado de la hipotenusa y obtener su valor real.
¿Qué letra se usa comúnmente para representar la distancia entre dos puntos?
-Generalmente se usa la letra 'd' para representar la distancia.
¿Qué pasos siguen después del cálculo para cerrar la explicación?
-El instructor invita a los estudiantes a ver el curso completo y a interactuar con el video (like, compartir, comentar).
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

1. Distancia entre dos puntos. Deducción de la fórmula y ejemplos

Distancia entre dos puntos, usando Teorema de Pitágoras

Distancia Entre Dos Puntos En El Plano Cartesiano

Distancia entre dos puntos | Demostración de la fórmula

DISTANCIA ENTRE DOS PUNTOS DEL PLANO: DEMOSTRACIÓN Y EJEMPLO
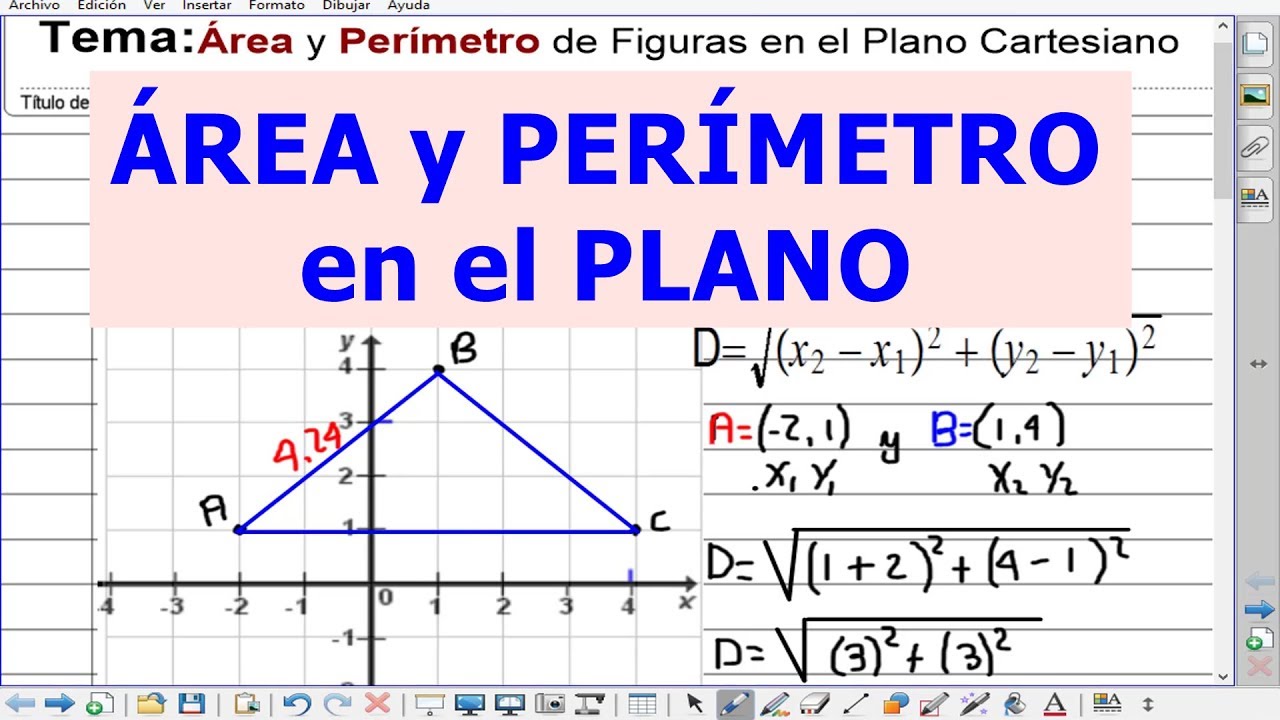
Área y Perímetro de Figuras en el Plano Cartesiano.
5.0 / 5 (0 votes)
