Daerah Asal Alami Fungsi Rasional dan Fungsi Irasional - Matematika SMA Kelas XI Kurikulum Merdeka
Summary
TLDRThis video lesson continues the exploration of high school mathematics, specifically for the 11th-grade curriculum under the Merdeka syllabus. The focus is on understanding the natural domain of functions, which is the set of all real numbers that make a function defined and its values determinable. The tutorial explains how to determine the natural domain for two types of functions: irrational functions in the form of square roots, where the domain is all real numbers for which the expression under the root is non-negative, and rational functions in fractional form, where the domain excludes any real numbers that would make the denominator zero. Examples are provided to illustrate the process of finding the domain for given functions, emphasizing the importance of real number values for a function to be well-defined.
Takeaways
- 📚 The video is a mathematics lesson for class 11, continuing the discussion on the concept of functions, specifically focusing on the natural domain of a function.
- 🔍 The natural domain of a function is determined by all real numbers that can make the function defined, meaning the range of possible input values that yield real output values.
- 🌐 The video explains the natural domain in terms of two types of rational functions: those in the form of roots and those in fractional form.
- 📐 For functions in root form, like √P(x), the domain is all real numbers where P(x) is greater than or equal to zero, ensuring the function is defined and the output is real.
- 🌰 An example is given where the function f(x) = √(x - 3) is defined for all x greater than or equal to 3, as the expression inside the root (x - 3) must be non-negative.
- 📉 The process of determining the domain involves analyzing the function and finding the boundary values of x that satisfy the condition for the function to be defined.
- 🚫 It's emphasized that for a function in fractional form, like P(x)/Q(x), the domain excludes values of x that would make the denominator Q(x) equal to zero, as division by zero is undefined.
- 📝 The video provides a method to determine the domain by setting up an inequality that excludes values causing the denominator to be zero, as shown with the function f(x) = (x + 4) / (3x - 9), where x cannot be 3.
- 📚 The lesson includes practical examples and exercises to help students understand how to find the natural domain of different types of functions.
- 💡 The importance of understanding the natural domain is highlighted for correctly applying and interpreting mathematical functions.
- 👨🏫 The instructor encourages students to practice and share their solutions in the comments section for further learning and engagement.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is the concept of the natural domain of a function in the context of high school mathematics for grade 11, specifically focusing on rational and radical functions.
What is the natural domain of a function?
-The natural domain of a function is the set of all real numbers that make the function defined or for which the function's value can be determined as a real number.
How is the natural domain determined for a radical function?
-For a radical function, the natural domain is determined by ensuring that the expression under the radical (denoted as 'px' in the script) is greater than or equal to zero.
What is an example of a radical function and its domain?
-An example given in the script is the function f(x) = √(x - 3). The domain of this function is all real numbers x such that x - 3 ≥ 0, which simplifies to x ≥ 3.
Why can't the expression under a radical be negative?
-The expression under a radical cannot be negative because the square root of a negative number is not a real number, and the natural domain consists of real numbers only.
What is the condition for the domain of a rational function?
-For a rational function, which is a fraction, the domain is determined by ensuring that the denominator (denoted as 'qx' in the script) is not equal to zero to avoid undefined expressions.
Can you provide an example of a rational function and explain how to find its domain?
-An example given is the function f(x) = (x + 4) / (3x - 9). To find its domain, we need to ensure that the denominator, 3x - 9, is not equal to zero, which leads to the condition x ≠ 3.
Why is it important to know the domain of a function?
-Knowing the domain of a function is important because it tells us the set of all possible input values (x-values) for which the function is defined and can produce real output values.
How does the script illustrate the process of finding the domain of a function?
-The script illustrates the process by providing step-by-step explanations and examples for both radical and rational functions, including the algebraic manipulation needed to find the conditions that define the domain.
What is the significance of the phrase 'natural domain' in mathematics?
-The term 'natural domain' refers to the most basic or widest set of input values for which a function is defined without any additional restrictions, typically the set of all real numbers unless specified otherwise.
How can students apply the concepts discussed in the script to solve related problems?
-Students can apply these concepts by identifying the type of function they are dealing with, setting up the appropriate inequality or condition based on whether it's a radical or rational function, and solving for the variable to find the domain.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
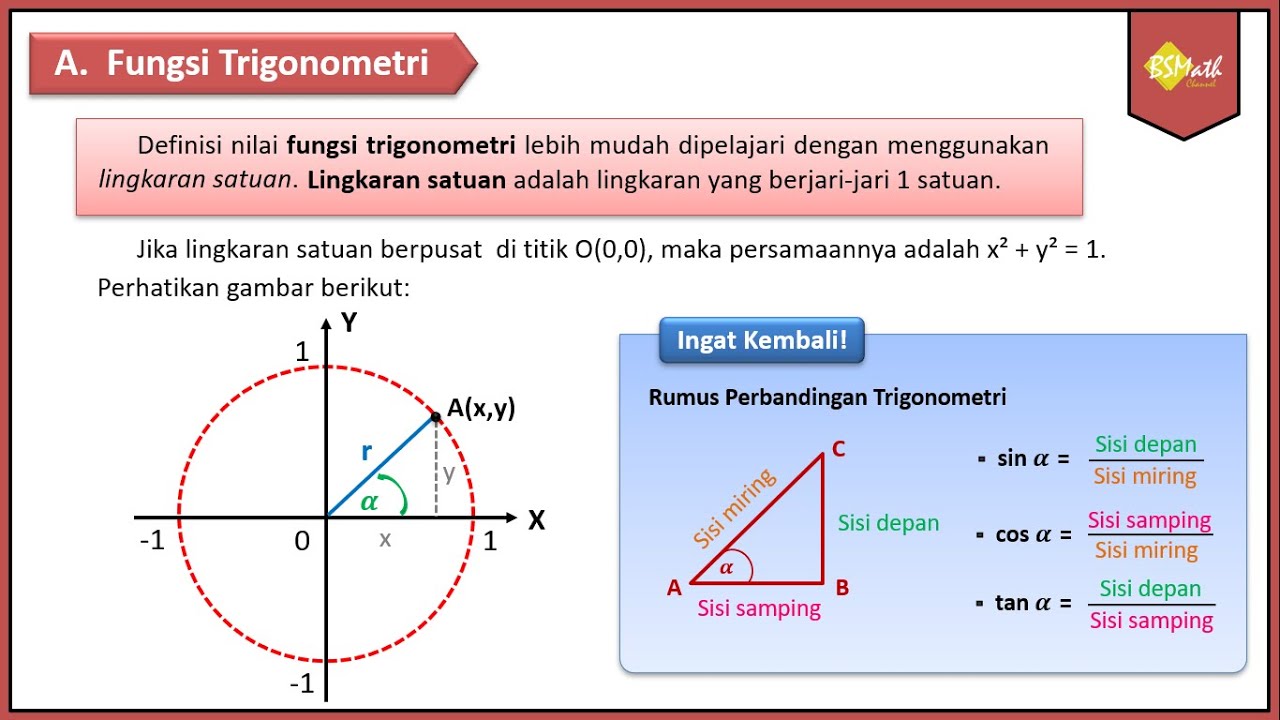
Tanda Fungsi Trigonometri Tiap Kuadran | Matematika Tingkat Lanjut SMA Kelas XI Kurikulum Merdeka

Garis Singgung Lingkaran Soal HOTS

Materi Matematika Kelas X Kurikulum Merdeka!! (Semester 2)

BAB 2 KEANEKARAGAMAN HAYATI | GEOGRAFI SMA KELAS XI | KURIKUKUM MERDEKA
(Part 1) FUNGSI KOMPOSISI DAN FUNGSI INVERS MATEMATIKA SMA KELAS 11 #kurikulummerdeka #matematikasma

Informatika kelas XI Kurikulum Merdeka
5.0 / 5 (0 votes)
