(Part 1) Definisi Lingkaran BAB LINGKARAN DAN GARIS SINGGUNG || Matematika Tingkat Lanjut Kelas XII
Summary
TLDRIn this video, viewers are introduced to the concepts of circles and tangents. The tutorial covers key topics such as the definition of a circle, the relationship between the center and radius, and how to derive the equation of a circle both with the center at (0,0) and at other coordinates. The video further explains how to use examples involving radius, diameter, and points on the circle to find the equation. Additionally, the general form of the circle's equation is explored, helping students understand the mathematical relationships between the center, radius, and the circle's equation.
Takeaways
- 😀 A circle is defined as a collection of points that are equidistant from a center point.
- 😀 The distance from the center to any point on the circle is called the radius.
- 😀 The general equation of a circle with its center at (0,0) is x² + y² = r².
- 😀 To find the equation of a circle with center (0,0), substitute the radius into the equation x² + y² = r².
- 😀 If given a diameter, the radius can be found by dividing the diameter by 2 before substituting into the circle equation.
- 😀 If the center is at (A,B), the equation of the circle becomes (x - A)² + (y - B)² = r².
- 😀 To find the equation of a circle that passes through a given point, calculate the radius by using the distance formula from the center to the point.
- 😀 When the center is not at (0,0), the formula (x - A)² + (y - B)² = r² is used to represent the circle's equation.
- 😀 The general form of the circle equation is x² + y² + ax + by + c = 0.
- 😀 Converting the equation from standard form to general form involves expanding and simplifying terms.
Q & A
What is the definition of a circle as presented in the script?
-A circle is a flat shape consisting of a collection of points that are all the same distance from its center point. This distance is known as the radius.
What is the general equation of a circle when the center is at the origin (0,0)?
-The equation of a circle centered at (0,0) with radius R is x² + y² = r².
How do you find the equation of a circle if the center is at a point other than (0,0)?
-For a circle with center at point (A, B) and radius R, the equation is (x - A)² + (y - B)² = r².
What is the first example provided in the script about finding the equation of a circle?
-The first example involves a circle with center at (0,0) and radius 6. The equation is x² + y² = 36 after substituting the radius squared (6² = 36).
How do you calculate the radius of a circle when given the diameter?
-To find the radius from the diameter, divide the diameter by 2. For example, if the diameter is 4√3, the radius is 2√3.
In the example where Andi needs to determine the equation of a circle through point T (6, -8), what is the radius of the circle?
-The radius is 10, calculated using the formula x² + y² = r², where x = 6 and y = -8, resulting in r² = 6² + (-8)² = 100, so r = 10.
What is the general form of a circle's equation?
-The general form of a circle's equation is x² + y² + ax + by + c = 0, where a, b, and c are constants related to the circle's center and radius.
What is the equation of a circle with center at point (1,2) and radius 6?
-The equation is (x - 1)² + (y - 2)² = 36, where the center is (1,2) and the radius is 6.
How do you convert the equation of a circle from its standard form to the general form?
-To convert to the general form, expand the squared terms and simplify. For example, (x + 1)² + (y - 2)² = 9 becomes x² + 2x + 1 + y² - 4y + 4 = 9, which simplifies to x² + y² + 2x - 4y - 4 = 0.
In the general form equation, how do you determine the values of a, b, and c from the expanded form?
-From the expanded form of the circle equation, the values of a, b, and c can be found using the relations: a = -2x, b = -2y, and c = x² + y² - r².
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Southeast Asian Mathematical Olympiad Competition (SEAMO) Training 2022 - Paper D

Garis Singgung Lingkaran(2) - Garis Singgung Persekutuan Luar dan Dalam | Matematika Kelas 8 SMP MTs

Garis Singgung Lingkaran | Matematika SMA Kelas XI
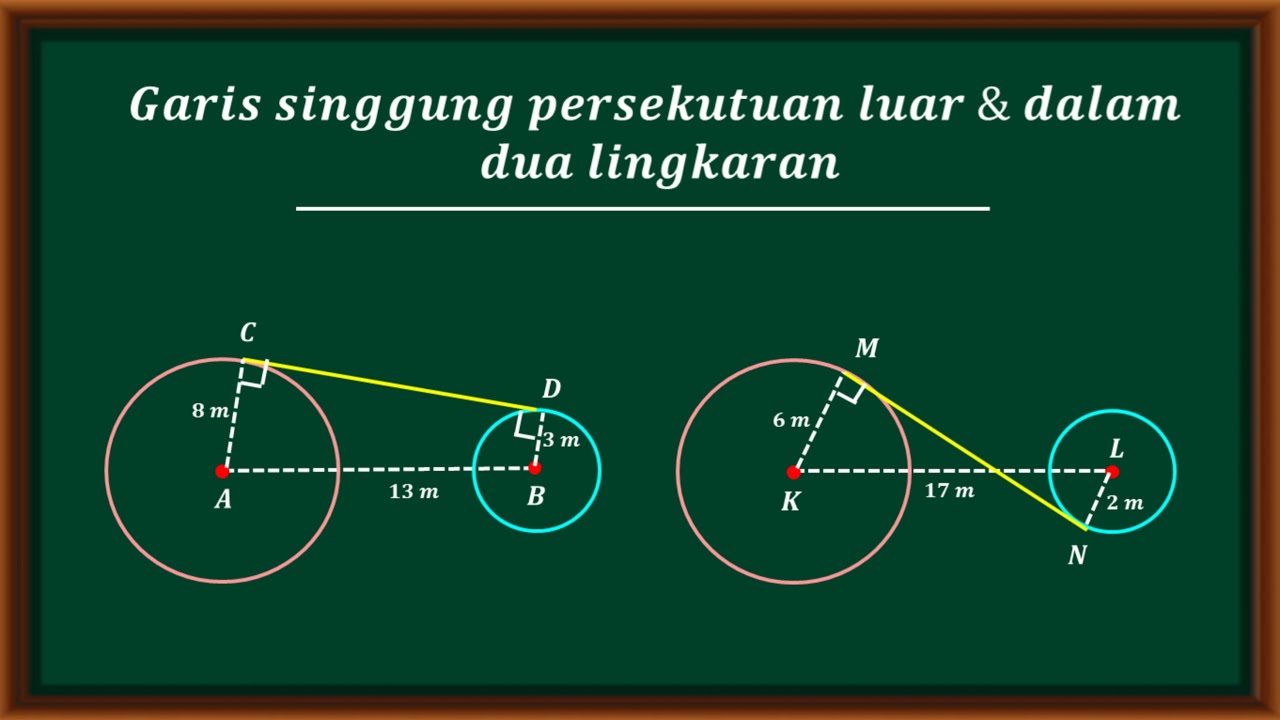
Garis singgung persekutuan luar dan garis singgung persekutuan dalam dua lingkaran
Garis Singgung Lingkaran (2) - Garis Singgung Persekutuan Luar dan Dalam - Matematika SMP

12-5 Angle Relationships in Circles
5.0 / 5 (0 votes)
