Garis Singgung Lingkaran(2) - Garis Singgung Persekutuan Luar dan Dalam | Matematika Kelas 8 SMP MTs

Summary

This video tutorial explains how to calculate the lengths of external and internal common tangents between two circles. It introduces key concepts and formulas, such as the external tangent formula (GSPL) and internal tangent formula (GSPD), which involve applying the Pythagorean theorem. The tutorial includes step-by-step examples to help viewers understand how to solve problems involving circle tangents using these formulas. Tips for approximating square roots of non-perfect squares are also provided to enhance problem-solving accuracy.

Takeaways

• 😀 The lesson covers the concept of tangent lines between two circles, focusing on two types: External Tangent Line (GSPL) and Internal Tangent Line (GSPD).
• 😀 External Tangent Line (GSPL) is a tangent line that touches both circles at different points outside the circles, and the distance between their centers is used in its calculation.
• 😀 The formula for GSPL is derived using the Pythagorean theorem, which requires the square of the distance between the centers of the circles (D) and the difference in their radii.
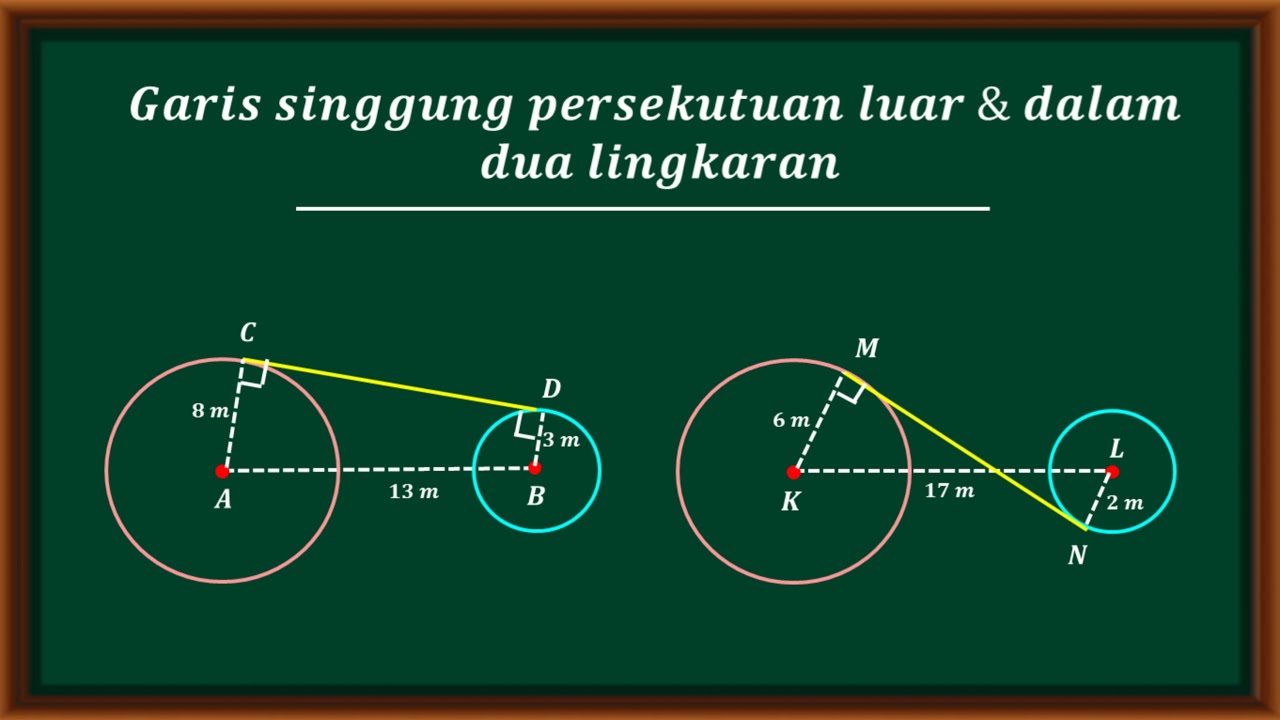
• 😀 The formula for GSPL is: GSPL = √(D² - (R1 - R2)²), where D is the distance between the circle centers, and R1 and R2 are the radii of the two circles.
• 😀 Internal Tangent Line (GSPD) is a tangent line that touches both circles from the inside, with the circles' radii being added in its formula.
• 😀 The formula for GSPD is: GSPD = √(D² - (R1 + R2)²), where D is the distance between the centers and R1 and R2 are the radii of the two circles.
• 😀 For solving tangent line problems, the distance between the centers of the two circles and the radii are crucial values needed for applying the formulas.
• 😀 Example problems show how to calculate the length of external and internal tangent lines given the radius values and the distance between the centers.
• 😀 In cases where the result involves a non-perfect square root, approximations can be made by identifying the nearest perfect squares and calculating the decimal value.
• 😀 The lesson emphasizes understanding the difference between external and internal tangents and using the correct formula based on the problem type.

Q & A

What is the formula used to calculate the length of the external common tangent (GSPL) between two circles?

The formula for the length of the external common tangent (GSPL) is: GSPL = √(D² - (R1 - R2)²), where D is the distance between the centers of the two circles, and R1 and R2 are the radii of the two circles.

How do you calculate the length of the internal common tangent (GSPD) between two circles?

To calculate the internal common tangent (GSPD), the formula is: GSPD = √(D² - (R1 + R2)²), where D is the distance between the centers of the two circles, and R1 and R2 are the radii of the two circles.

What is the significance of using the Pythagorean theorem in these calculations?

The Pythagorean theorem is used to form right-angled triangles when the centers of the circles and the points of tangency are connected. This helps in calculating the lengths of the tangents using the relationship between the sides of a right-angled triangle.

How does the difference in radii affect the formula for the external common tangent?

In the case of the external common tangent, the difference between the radii (R1 - R2) is subtracted from the square of the distance between the centers (D²) before taking the square root. This reflects the fact that the external tangent is influenced by the gap between the circles.

Why is the sum of the radii used in the formula for the internal common tangent?

The sum of the radii (R1 + R2) is used in the formula for the internal common tangent because the tangent line passes between the circles, where the radii are effectively added together to form the distance that affects the tangent's length.

What is the process to calculate the length of a tangent when the result is not a perfect square?

When the result is not a perfect square, approximate methods such as estimating the square root between two known perfect squares are used. For example, if √287 is needed, one would find the closest perfect squares (256 and 289) and then approximate the square root.

In the example with two circles of radii 14 cm and 4 cm, how is the internal common tangent calculated?

For the circles with radii 14 cm and 4 cm, and a center-to-center distance of 30 cm, the internal tangent is calculated using the formula: GSPD = √(30² - (14 + 4)²) = √(900 - 324) = √576 = 24 cm.

What is the result for the external common tangent when two circles with radii 7 cm and 2 cm are 13 cm apart?

For two circles with radii 7 cm and 2 cm, and a center-to-center distance of 13 cm, the external common tangent is calculated using the formula: GSPL = √(13² - (7 - 2)²) = √(169 - 25) = √144 = 12 cm.

What happens if the difference between the radii of the two circles is greater than the distance between their centers?

If the difference between the radii is greater than the distance between the centers, the two circles will overlap, and no common tangents (either internal or external) will exist. The formula will result in a negative value inside the square root, which is mathematically impossible.

What does the 'D' symbol represent in the formulas for common tangents?

'D' represents the distance between the centers of the two circles. It is a key variable in both the external and internal tangent formulas, affecting the length of the tangent lines based on the proximity of the circles.